Geometrie zum Jahresende - Lösung

[ottogal]

Hallo in die Runde, und gute Wünsche für 2019!

Meine ausführliche Lösung:

Zu 1.:
Die ganze Figur ist rotationssymmetrisch, also auch das innere Dreieck. (Sie bzw. es geht bei Drehung um 120° in sich selbst über.)

Zu 2.:

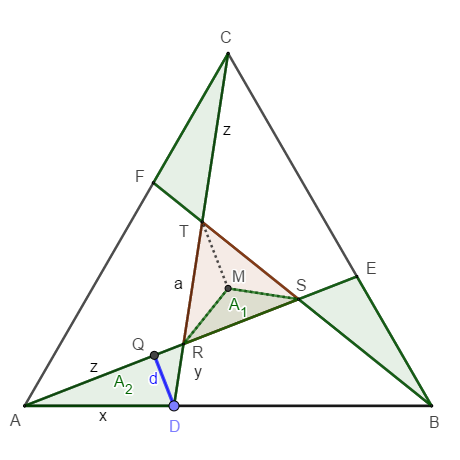
O.B.d.A. sei $$AB=1$$. Wir setzen $$AD=x$$ (sinnvoll ist $$0 \le x \le \frac{1}{2}$$), $$DR=y$$, $$RA=z$$, $$RT=a$$.

Die Dreiecke $$\triangle ADC$$ und $$\triangle RDA$$ sind zueinander ähnlich, da sie in den Winkeln übereinstimmen.
Daher ist $$\frac{AD}{AC}=\frac{RD}{RA}$$, d.h. $$\frac{x}{1}=\frac{y}{z}$$ und somit $$y=xz$$.

Für die Flächeninhalte gilt:

$$A_0=A_{ABC}=\frac{\sqrt 3}{4}$$;

$$3 \cdot A_1=A_{RST}=\frac{\sqrt 3}{4} a^2=A_0 \cdot a^2$$.

Da $$\triangle DRQ$$ ein halbes gleichseitiges Dreieck (mit der Höhe $$d=DQ$$) ist, folgt

$$d=\frac{\sqrt 3}{2} y=\frac{\sqrt 3}{2} xz$$ und damit

$$A_2=A_{RAD}=\frac{1}{2} z \cdot d=\frac{\sqrt 3}{4} xz^2= A_0 \cdot xz^2$$.

Die Dreiecke $$\triangle ADC$$ und $$\triangle ABC$$ haben die Höhe gemeinsam, daher gilt

$$\frac{A_{ADC}}{A_{ABC}}=\frac{x}{1}$$, also $$A_{ADC}=A_0 \cdot x$$.

Damit folgt $$A_{ARC}=A_0 \cdot x - A_2=A_0 \cdot x (1-z^2)$$ und für das innere gleichseitige Dreieck:

$$A_{RST}=A_0-3 \cdot A_{ARC}=A_0(1-3x(1-z^2))$$.

Das Flächenverhältnis von innerem zu äußerem gleichseitigen Dreieck ist also

$$\frac{A_{RST}}{A_0}=1-3x(1-z^2)$$.

Nun gilt aber $$\frac{A_{RST}}{A_0}=a^2$$ (siehe oben). Damit erhalten wir die folgende

Beziehung zwischen den Größen $$a$$, $$x$$ und $$z$$:

|$$(1-a^2)=3x \cdot (1-z^2)$$|

Dies gilt allgemein für jeden Wert im Bereich $$0 \le x \le \frac{1}{2}$$.

Der Spezialfall:

Aus dieser Gleichung erkennt man: $$a=z$$ genau dann, wenn $$x=\frac{1}{3}$$.

Die Vermutung (bzw. Hoffnung): $$x=\frac{1}{3}$$ ist der gesuchte Wert, um das Flächenverhältnis $$a^2=\frac{1}{7}$$ zu erhalten.

Vor.: $$x=\frac{1}{3}$$

Beh.: $$a^2=\frac{1}{7}$$

Beweis:

Mit der Voraussetzung wird aus der obigen Gleichung $$a^2=z^2$$, also $$a=z$$ und mit $$y=xz=xa$$:

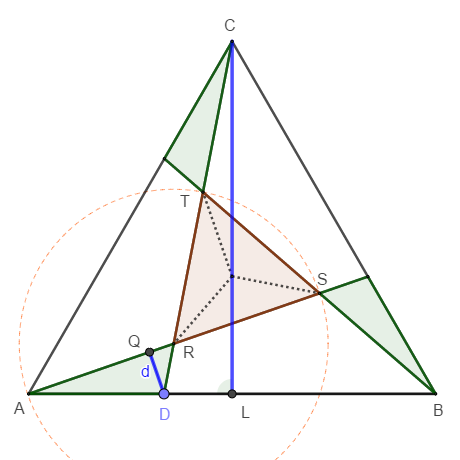
$$CD=z+a+y=a(2+x)=a(2+\frac{1}{3})=\frac{7}{3} a$$.

Pythagoras im $$\triangle CDL$$ liefert wegen $$DL=\frac{1}{2}-x=\frac{1}{6}$$:

$$CD^2=(\frac{1}{6})^2+(\frac{\sqrt 3}{2})^2=\frac{7}{9}$$.

Der Vergleich ergibt $$(\frac{7}{3} a)^2=\frac{7}{9}$$,

und daher, wie behauptet, $$a^2=\frac{1}{7}$$.

Nachbemerkung

Zur Zerlegung in 21 flächengleiche Teildreiecke (im Spezialfall $$x=\frac{1}{3}$$):

Die Dreiecke $$\triangle ARD$$ und $$\triangle RSM$$ haben die gleiche Grundseite ($$z$$ bzw. $$a$$) und die gleiche Höhe $$d=\frac{\sqrt 3}{2} xz=\frac{\sqrt 3}{6} a$$; denn dies ist ein Drittel der Höhe von $$\triangle RST$$, da im gleichseitigen Dreieck die Höhen auch die Schwerlinien sind und sich daher im Verhältnis 2:1 schneiden.

Ansonsten ergibt sich die Flächengleichheit der Teildreiecke wegen Übereinstimmung von Grundseite und Höhe (und wegen $$y:z=1:3$$).