Hallo in die Runde,
bei mir ist nur von Gunnar eine Lösung eingegangen (schon nach wenigen Stunden).
Vielleicht ist es das Abdriften des Threads, vielleicht auch der vorweihnachtliche Stress allenthalben, der weitere Beteiligung verhindert hat.
Jedenfalls denke ich, es ist Zeit zum Auflösen.
Gunnar hat den Kreis in ein Kartesisches Koordinatensystem gelegt, für die 4 fraglichen Verbindungen Geradengleichungen aufgestellt und paarweise einige ihrer Schnittpunkte berechnet. Übereinstimmende Ergebnisse beweisen die Aussage. Das ist völlig in Ordnung; Descartes ist ja nicht ohne Grund berühmt geworden...
Mir ist aber bei solchen Aufgaben ein elementargeometrischer Beweis lieber.
Meine Lösung sieht so aus:
Vorbetrachtung
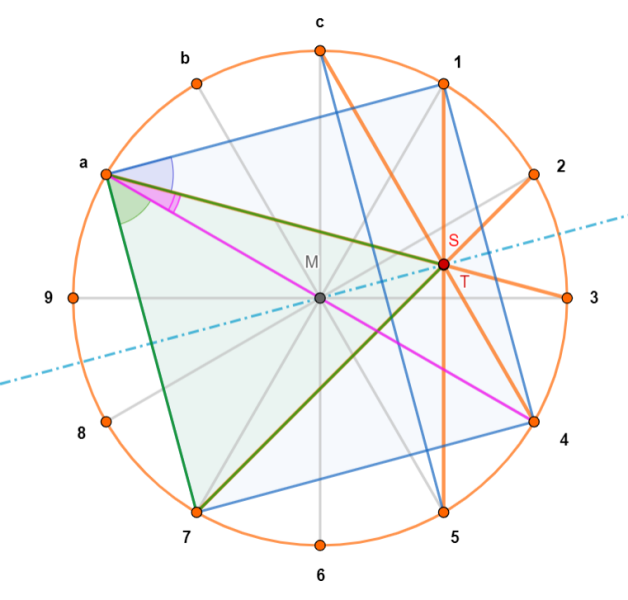
Die goldenen Punkte benennen wir wie auf dem Zifferblatt einer Uhr, wobei wir der Kürze halber statt der zweistelligen Zahlen 10 bis 12 die Hex-Ziffern a, b und c verwenden (womit die hier Mitlesenden kein Problem haben sollten).
Zwei benachbarte goldene Punkte bestimmen mit den Radien jeweils einen Kreissektor mit dem Mittelpunktswinkel 30° (z.B. den Sektor M65). Der dazugehörige Umfangswinkel ist halb so groß, also z.B. $$\angle{4a3}=15°$$ (pinkfarbig).
Umfangswinkel zu doppelt (bzw. dreifach) so großen Kreisbögen sind entsprechend doppelt (bzw. dreifach) so groß, z.B.
$$\angle{3a1}=30°$$ (blau) und $$\angle{7a4}=45°$$ (grün).
Lösung
Das Viereck 741a ist ein Quadrat. Die Mittelsenkrechte von a7 ist Symmetrieachse der gesamten Figur.
Insbesondere liegen die Strecken 15 und 4c symmetrisch zueinander, ebenso die Strecken a3 und 72.
Sei S der Schnittpunkt von 15 mit der Symmetrieachse und
T der Schnittpunkt von a3 mit der Symmetrieachse.
Zu zeigen ist: T und S sind der selbe Punkt.
Als Achsenpunkt wird S auf sich selbst gespiegelt, muss also auch auf dem Spiegelbild 4c von 15 liegen.
Als Achsenpunkt wird T auf sich selbst gespiegelt, muss also auch auf dem Spiegelbild 72 von a3 liegen.
Nach der Vorbetrachtung über Winkel ist $$\triangle{a7T}$$ gleichseitig.
Daher ist das $$\triangle{4T7}$$ gleichschenklig, die Basiswinkel haben 75°.
Also ist $$\angle{T47}=75°$$ und daher $$\angle{14T}=15°$$.
Nun ist aber auch $$\angle{14c}=15°$$. Deshalb muss T auf dem Winkelschenkel 4c liegen, als Achsenpunkt muss er also der Schnittpunkt von 4c mit der Achse sein. Das ist aber der Punkt S.
q.e.d.
Viele Grüße
ottogal