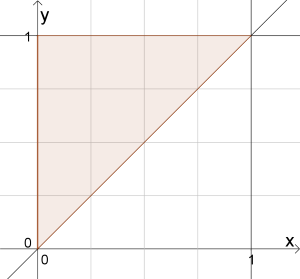Dann will ich auch mal. Meine Lösung ist ANDERS, aber ich behaupte mal: im Rahmen der Aufgabenstellung nicht falsch. Ich verwende eine andere Vorgehensweise für die zufällige Aufteilung und komme damit auf andere Wahrscheinlichkeiten.
Dank Gunnars Monte-Carlo-Vorlage kann ich experimentell nachweisen, dass ich mich nicht verrechnet habe (wie Matthias Apsel zunächst vermutet hat). Es ist einfach die andere Teilungslogik.
In euren Methoden habt ihr zwei beliebige Punkte auf die Linie gesetzt. Ich dagegen habe die Sägewerkmethode angewendet: Da ist 'ne Latte, davon schneide ich mal ein Stück ab, das lege ich weg und den Rest säge ich irgendwo durch.
In Gunnars Monte-Carlo-Script bedeutet das: Ich ersetze
x = Math.random();
y = Math.random();
durch
x = Math.random();
y = x + Math.random()*(1-x);
Nun meine Lösung auf dieser Grundlage:
Unsere Strecke sieht so aus:
|-----a-----|---b--|----c----|
0 A B L
wobei natürlich Punkte zusammenfallen können, es war keine Mindestlänge für die Segmente vorgegeben. Für die Rechnung nehme ich oBdA an, dass die Strecke die Länge 1 hat.
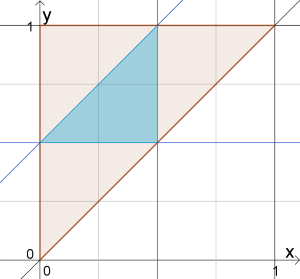
Für die zufällige Unterteilung setze ich den Punkt A zufällig ins Intervall $$[0,1]$$ und habe mein Segment a, dann setze ich den Punkt B zufällig ins Intervall $$[A,1]$$ und habe die Segmente b und c. Auf Grund der Konstruktion gilt $$a\geqq0, b\geqq0, c\geqq0$$ und $$a+b+c=1$$ (bzw. $$b+c=1-a$$).
Ein Dreick kann nicht gezeichnet werden, wenn die Summe der Längen zweier Seiten kleiner ist als die dritte Seite, also für $$a > b+c$$, $$b > a+c$$ oder $$c > a+b$$. Im konkreten Fall bedeutet das: Ist eine Seite länger als 0,5, geht es nicht. Ich mache keine Sonderbetrachtung dafür, dass eine Teilstrecke die Länge 0 hat, das ist nicht nötig. Das Dreieck entartet dann lediglich zu einem Strich.
Ich bilde nun eine Funktion w(a) über dem Intervall $$[0,1]$$, die mir angibt, mit welcher Wahrscheinlichkeit für dieses a ein Dreieck möglich ist. Für a in $$]\frac{1}{2}, 1]$$ ist w(a), wie beschrieben, 0.
Für den Fall $$a \leqq 0,5$$ hat die verbleibende Strecke die Länge 1-a und wird von B in zwei Teile geteilt. Für die Lage von B gibt es drei Zonen. Ist $$b > 0,5$$, so ist ein Dreieck nicht möglich (rechte xxxx Zone). Ist es kleiner als $$0,5-a$$, dann ist $$c > 0,5$$ und ebenfalls kein Dreieck möglich (linke xxxx Zone). Der Wert $$0,5 - a$$ errechnet sich aus $$1-a - 0,5$$.
|xxxxxx|-----------------|xxxxxx|
0 0,5-a 0,5 1-a
Wenn B gleichverteilt in den Bereich A bis 1 gesetzt wird, dann ist die Wahrscheinlichkeit, dass es in einem Abschnitt einer bestimmten Länge liegt, das Verhältnis der Längen von Abschnitt zu Gesamtstrecke, also:
$$\begin{align}p(b > 0,5) &= 1 - p(b \le 0,5) = 1 - \frac{0,5}{1-a}
&= \frac{0,5-a}{1-a}
p(b < 0,5-a) &= \frac{0,5-a}{1-a}
\end{align}$$
Die Wahrscheinlichkeit, dass für einen bestimmten Wert von a kein Dreieck möglich ist, beträgt also
$$\overline{w}(a) = 2 \cdot \frac{0,5-a}{1-a} = \frac{1-2a}{1-a}$$
oder andersherum, die Wahrscheinlichkeit, dass eins möglich ist, lautet
$$w(a) = 1 - \overline{w}(a) = 1 - \frac{1-2a}{1-a} = \frac{1-a-1+2a}{1-a}= \frac{a}{1-a}$$
Um über dem Intervall die Wahrscheinlichkeit zu bilden, muss man das integrieren:
$$\int_0^{0,5}\frac{a}{1-a}\mathrm d a$$
Hier quiescht der Rost in meiner Analysis, aber die Funktion ist bronstein-integrierbar, die Stammfunktion lautet
$$W(a) = -a - ln(1-a) + C$$
und damit beträgt die Wahrscheinlichkeit
$$\begin{align}
p(dreieck) &= W(0,5)-W(0)
& = -0,5 - ln(0,5) - (0-ln(1))
& \approx 19,3%
\end{align}$$
Die Lösung, die ich Matthias geschickt hatte, enthielt noch ein paar begriffliche Fehler, die wollte ich beseitigen. Und eigentlich bin ich nun erstaunt, dass ich auf ein sinnvolles Ergebnis gekommen bin. Denn mein w(a) hatte ich mir als eine Wahrscheinlichkeitsdichtefunktion vorgestellt. Es ist aber keine. Eine Dichtefunktion muss, wenn man sie von $$-\infty$$ bis $$+\infty$$ integriert, den Wert 1 ergeben. Das tut meine nicht. Ich weiß also nicht mehr genau, welches Statistikprinzip ich hier verwendet habe. Aber die Monte Carlo Probe sagt, dass das Ergebnis plausibel ist :)
Rolf
Matthias Apsel
Rolf b
Tabellenkalk
TS
Gunnar Bittersmann
Der-Dennis
JürgenB
MudGuard
