Hallo,

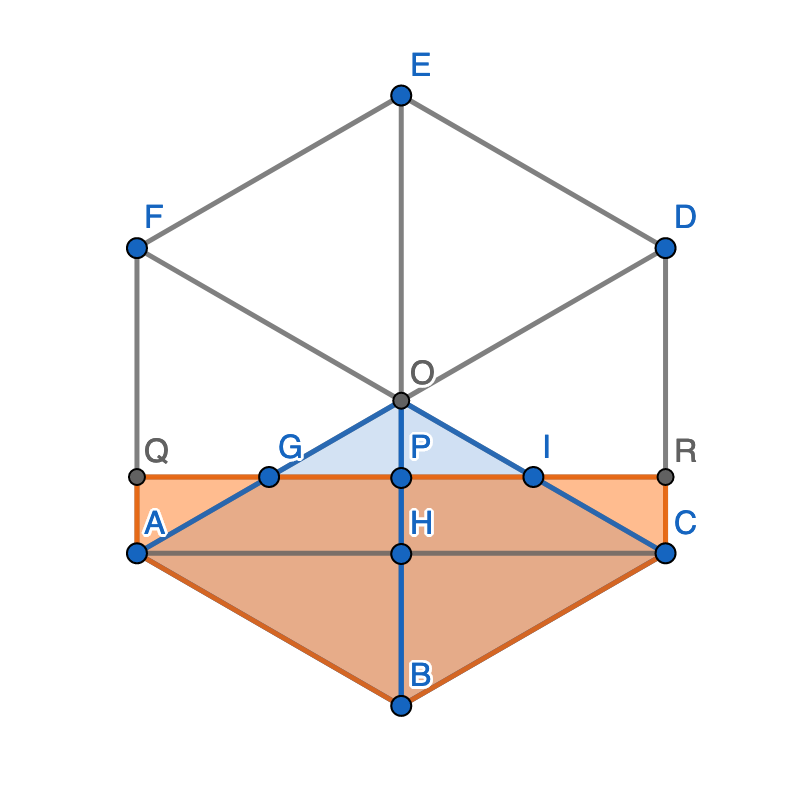
Wir teilen das Sechseck (Kantenlänge 1 o.B.d.A.) in 6 gleichseitige Dreiecke. Zwei davon (ABCO) haben ein Drittel der Fläche des Sechsecks.

G, H und I seien die Mittelpunkte von OA, OB und OC. Die Dreiecke AGQ und OGP sind kongruent nach WSW, damit OP = AQ = HP. Wegen OH = BH = ½ ist OP = ¼.

Ebenso sind die Dreiecke IOP und ICR kongruent. Damit sind ABCO und ABCRQ flächengleich; letzte ist also die schraffierte Fläche aus der Aufgabe.

BP : EP = (1 − ¼) : (1 + ¼) = 3 : 5

genau so hatte ich es auch hergeleitet, nur dass ich mich auf eine Hälfte des Sechsecks beschränkt habe - es ist ja symmetrisch z.B. zur senkrechten Mittelachse.

So long,
 Martin

PS: Was zum Geier heißt o.B.d.A.? Ohne Beißen des Autors?