iptables und seine Folgen

[1unitedpower]

Die Entropie von Passwörtern wird durch eine einfache Rechnung halt deutlich überschätzt.

Full ACK. Man kann (und sollte) meine urprüngliche Aussage also noch schärfer formulieren:

Um 2048 Bit Entropie zu erreichen, müsste ein ASCII-Passwort mindestens aus 256 Zeichen bestehen, de fakto müssen es noch wesentlich mehr sein, weil wegen den von dir genannten Gründen.

Auf der anderen Seite ist der tatsächliche Zeichenvorrat komplexitätstheoretisch(*) vernachlässigbar. Man nehme zum Beispiel ein Passwort der Länge 10 über 26 Buchstaben. Es gibt also 26^10 Möglichkeiten, ein Passwort zu wählen. Erhöht man bei gleichbleibender Länge den Zeichenvorrat auf 29 Zeichen, ergeben sich 29^10 Möglichkeiten. Fixiert man nun statt der Länge, das zugrunde liegende Alphabet und erhöht die Länge des Passworts um 3 Zeichen, ergeben sich 26^13 Kombinationsmöglichkeiten. Der Einfluss der Länge ist also exponentiell in der Größe des Zeichenvorrats beschränkt, der Einfluss des Zeichenvorrats ist dagegen nur linear in der Länge des Passworts beschränkt.

*) Soweit die Theorie. In der Praxis hat der Nutzer eigentlich nur die Möglichkeit die Länge zu varrieren und kann auf den Zeichenvorrat überhaupt keinen Einfluss nehmen.

Ein Comic sagt mehr als 1000 Worte:

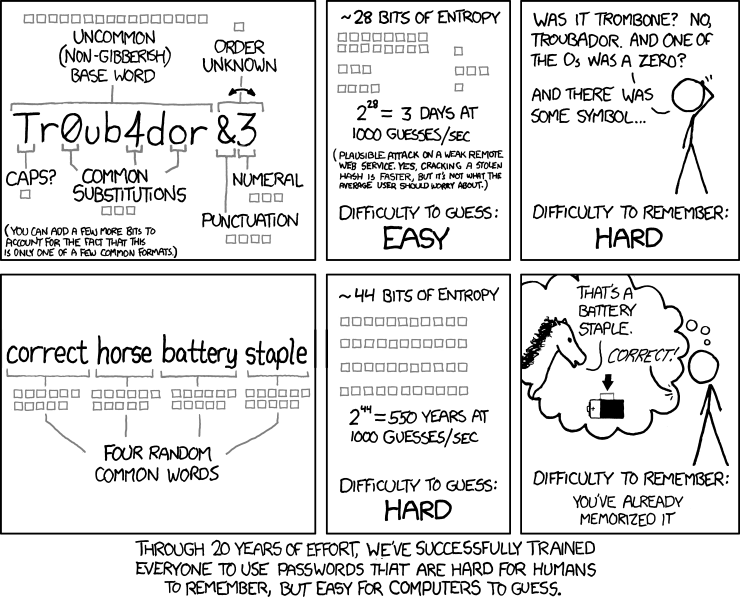
(Quelle: https://xkcd.com/936/)

Extended ASCII hätte 8 Bit pro Zeichen, aber auch darin kommen Steuerzeichen vor, die man bei exakter Rechnung noch berücksichtigen müsste.

Welche Version der Extension, ANSI, ISO-8852-15, …? ;-)

Diejenigen, die kompatibel mit den ersten 128 Zeichenkodierungen aus UTF-8 sind. Also die einzigen mit Existensberechtigung :P