Mathematik zum Wochenende

[ottogal]

(Edit: Ich habe bei den meisten Produkten den * für die Multiplikation weggelassen, da das hier manchmal automatisch geschieht. Konnte den vorherigen Post nicht mehr bearbeiten, kA weshalb.)

Meine Lösung

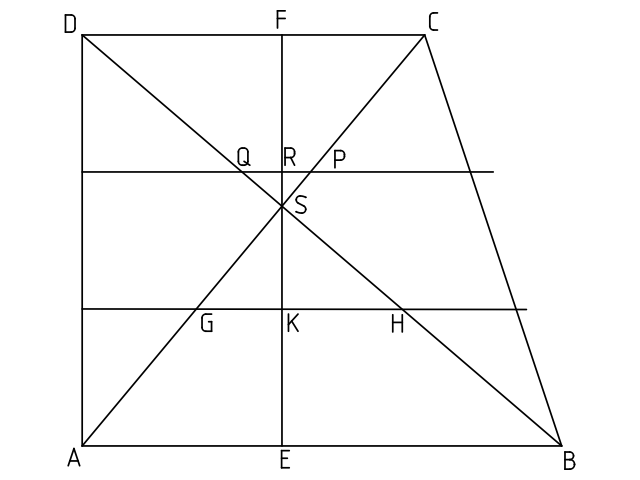
Der Diagonalenschnittpunkt des Trapezes heiße S. Die Trapezhöhe durch S sei EF (E auf AB, F auf CD). Die Endpunkte von p seien G und H, der Schnittpunkt von GH mit EF heiße K. Die Endpunkte von q seien Q und P, der Schnittpunkt von QP mit EF heiße R.

Beweis von c):

Sämtliche im Folgenden verwendeten Verhältnis-Gleichheiten folgen aus den Strahlensätzen mit dem Zentrum S. Zur Abkürzung bezeichnen wir das Verhältnis c/a mit k.

Man erhält:

SF/SE = SC/SA = c/a = k

SF = k SE

(1+k)SE = SE + SF = h

SE = h/(1+k)

SK = SE - h/3 = h( 1/(1+k) - 1/3 )

SK = h(2-k) / 3(1+k)

p/a = SG/SA = SK/SE = (1/SE) SK = (1+k)/h * (h(2-k) / 3(1+k)) = (2-k)/3

p = (2-k)a/3

Mit k = c/a wird daraus

p = (2a-c)/3

Aus SF = k SE folgt weiter:

SF= kh/(1+k)

SR = SF - RF = h( k/(1+k) - 1/3 )

SR = h*( 2k-1) / 3(1+k) )

q/c = PQ/CD = SP/SC = SR/SF = (2k-1)/3(1+k) / (1+k)/k = (2k-1) / 3k

q = c*(2k-1) / 3k = c*(2-1/k)/3

Mit 1/k = a/c wird daraus q = c*(2-a/c)/3, also

q = (2c-a)/3

Zu a): Aus den gegebenen Daten erhält man mit den gefundenen Formeln p = 3 und q = 1.

Zu b): Alle im obigen Beweis verwendeten Verhältnis-Gleichheiten gelten unabhängig vom Winkel ⍺.