@@Matthias Apsel
Beweisen Sie, dass für beliebige nicht negative Zahlen $$a$$, $$b$$, $$c$$ folgende Ungleichung gilt:
$$ a^2+b^2+c^2 \geq ab+ac+bc $$
Mit der Einschränkung auf nichtnegative Zahlen kann man das wunderschön ohne zu rechnen geometrisch beweisen:
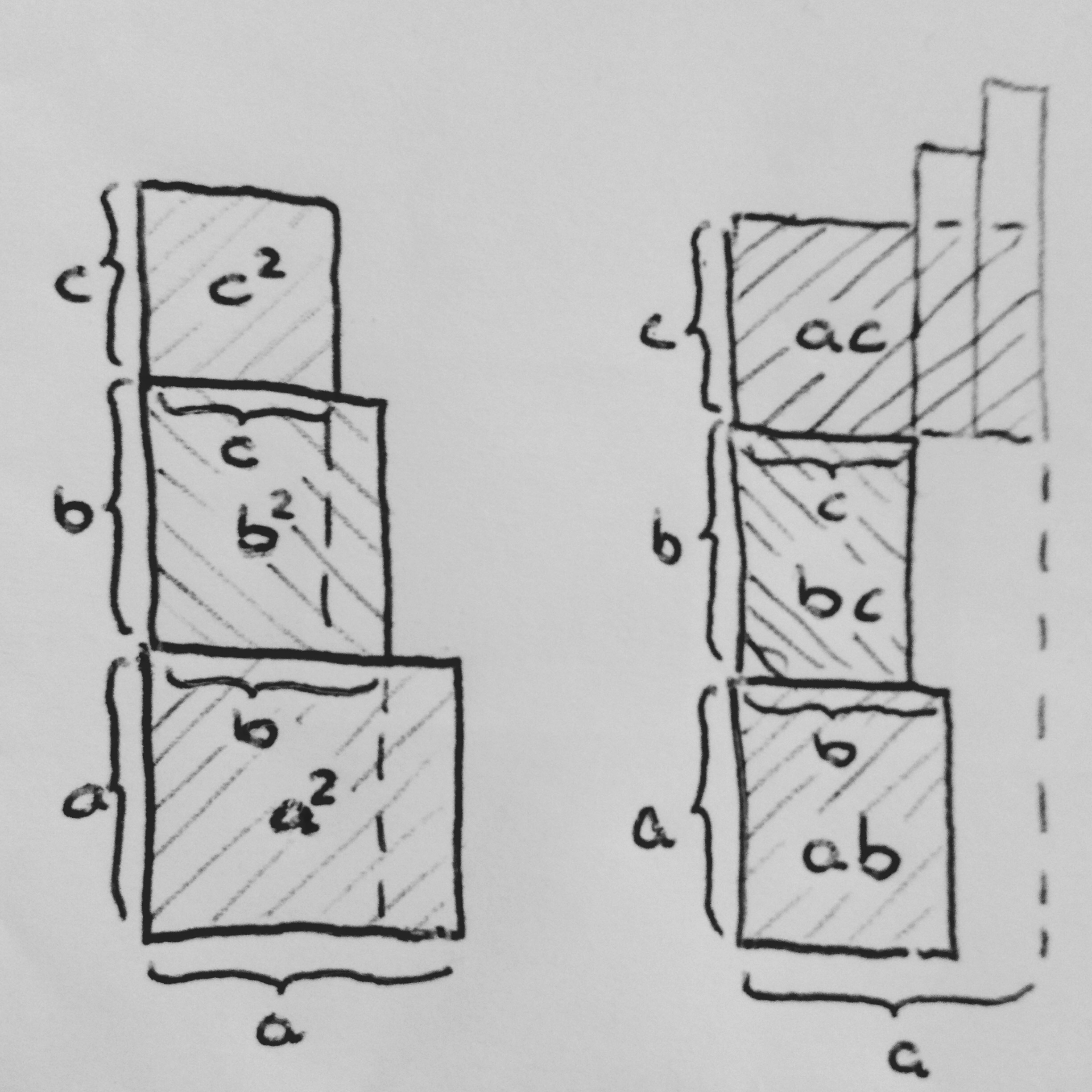
Es sei o.B.d.A. a ≥ b ≥ c
Man schneidet von den Quadraten die jeweils überstehenden Streifen ab und schiebt sie nach oben. (Bei Gleichheit zweier Längen gibt es halt keinen Streifen.) Schon sieht man die zu beweisende Ungleichung erfüllt.
LLAP 🖖
--
“I love to go to JS conferences to speak about how to avoid using JavaScript. Please learn CSS & HTML to reduce your JS code bloat.” —Estelle Weyl
“I love to go to JS conferences to speak about how to avoid using JavaScript. Please learn CSS & HTML to reduce your JS code bloat.” —Estelle Weyl


