Mathematik zum Wochenende

[Gunnar Bittersmann]

@@Matthias Apsel

42a Man zeige, dass

$$\frac{a}{b} + \frac{b}{a} \geq 2$$

Der algebraische Weg sollte offensichtlich sein. Es geht aber auch hier geometrisch, Strahlensatz reicht.

O.B.d.A. a ≥ b. Ich betrachte den Fall a ≥ b > 1:

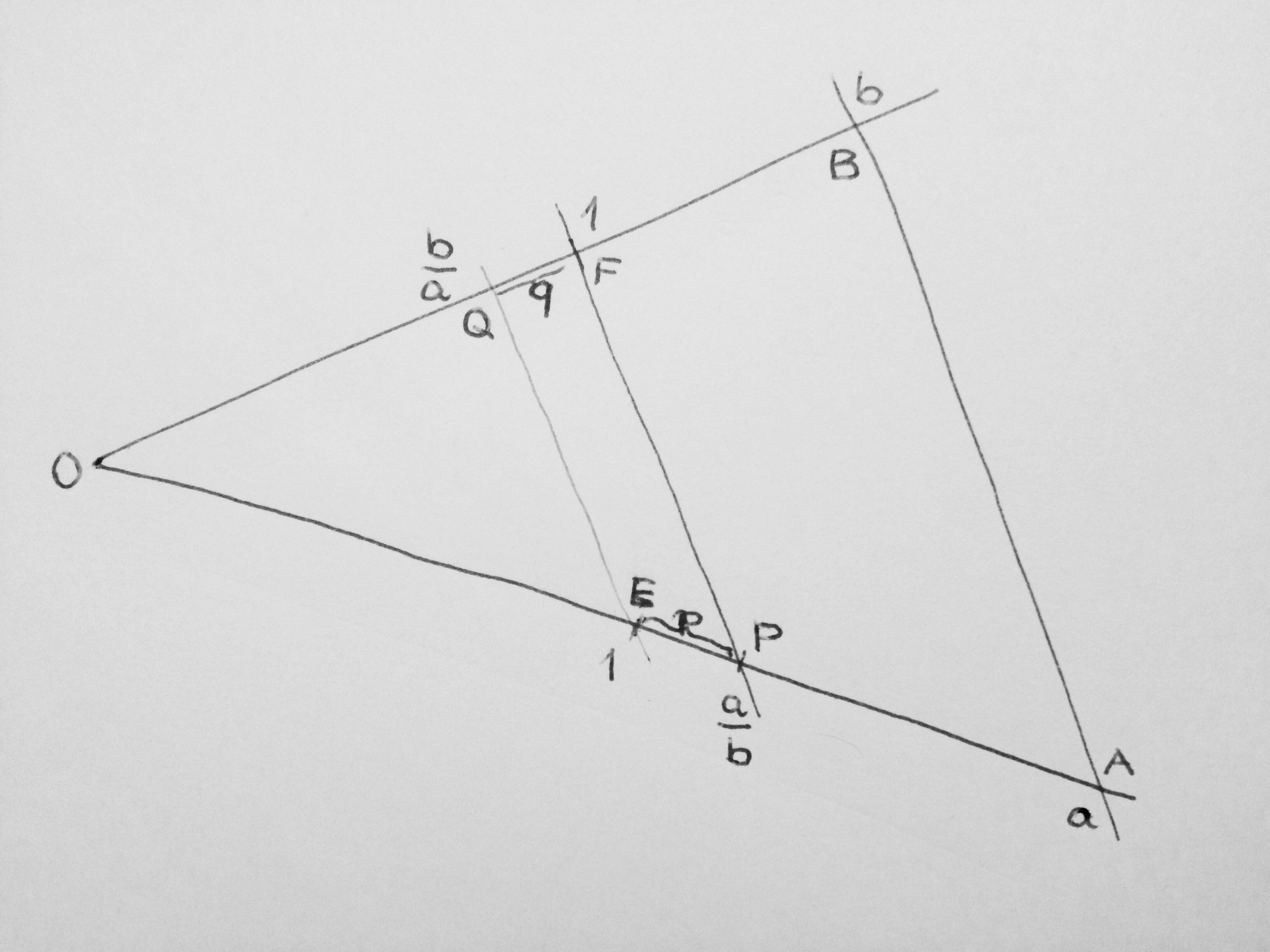
Die Punkte A und B liegen auf verschiedenen Schenkeln eines Winkels, so dass die Längen OA = a und OB = b sind. Die Punkte E und F sind jeweils eine Längeneinheit vom Scheitel entfernt: OE = OF = 1.

Die Parallele zu AB durch E schneide den anderen Schenkel in Q, die Parallele zu AB durch F schneide den anderen Schenkel in P.

Für a > b liegt P zwischen E und A und Q zwischen O und F. Die Längen seien EP = p und QF = q.

Für a = b fällt P mit E und Q mit F zusammen, d.h. p = q = 0.

Nach Strahlensatz gilt:
$$\frac{OP}{OF} = \frac{OA}{OB}$$, also $$\frac{OP}{1} = \frac{a}{b}$$
und
$$\frac{OQ}{OE} = \frac{OB}{OA}$$, also $$\frac{OQ}{1} = \frac{b}{a}$$

Außerdem:
$$\frac{EP}{QF} = \frac{OA}{OB}$$, also $$\frac{p}{q} = \frac{a}{b}$$, d.h. wegen a ≥ b gilt p ≥ q, also p − q ≥ 0.

Nun ist
OP + OQ = OE + EP + OF − QF, also $$\frac{a}{b} + \frac{b}{a} = 1 + p + 1 - q = 2 + p - q ≥ 2 + 0$$.

Entsprechend wären noch die Fälle a ≥ 1 ≥ b und 1 > a ≥ b zu betrachten.

LLAP 🖖