Lösung

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Der Publikumsjoker hilft hier auch nicht wirklich weiter …

Der Telefonjoker sagt, D scheidet aus. 😜

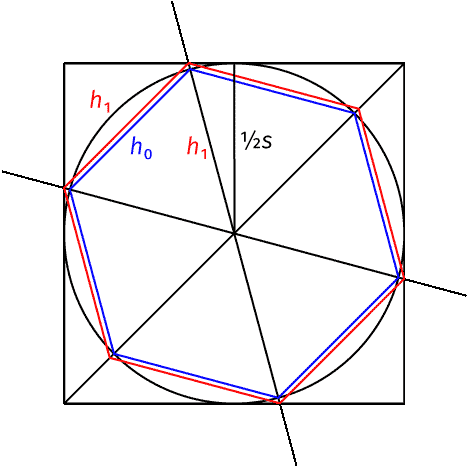
Den 50:50 heben wir uns für später auf. Malen wir das mal auf. In das Quadrat legen wir den größtmöglichen Kreis (Radius ½s) und auf diesen ein reguläres Sechseck, und zwar listigerweise so, dass zwei seiner Eckpunkte auf einer Diagonalen des Quadrats liegen (blau). Dieses Sechseck hat die Kantenlänge h₀ = ½s und seine Eckpunkte liegen allesamt im Inneren des Quadrats.

Es geht also größer. Wir strecken das Sechseck um den Mittelpunkt, so dass die vier Eckpunkte, die nicht auf der Diagonalen liegen, auf dem Rand des Quadrates zu liegen kommen (rot). Die Kantenlänge h₁ dieses Sechsecks ist größer als ½s, s < 2h₁

A ist also richtig.

Der Clou hieran ist: wir wissen nicht, ob dieses Sechseck das größtmögliche ist. Müssen wir auch gar nicht. Wenn es ein noch größeres Sechseck mit h > h₁ gibt, dann gilt erst recht s < 2h₁ < 2h.

---

Zusatzaufgabe: Untersuche, ob es ein solches größeres Sechseck gibt oder nicht, ob also h > h₁ oder h = h₁ gilt.

LLAP 🖖