Lösung

[Gunnar Bittersmann]

@@Gunnar Bittersmann

So, die wären dann auch weg. Es geht komplett ohne Wurzeln. Sag ich doch.

Und zwar so:

Sei a = AB = BC die Seitenlänge das Achtecks; b = KA = KB wie in meiner nicht so einfachen Lösung im anderen Thread. Der Radius des Kreises sei r = KC = KS; der Streckenabschnitt x = BS.

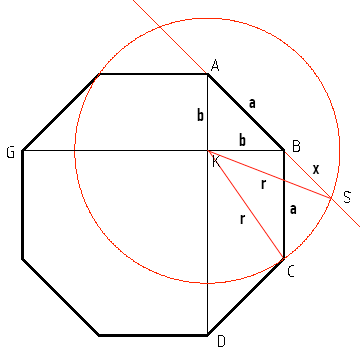
Pythagoras im Dreieck BAK: a² = 2b², also b² = ½a² (1)

Pythagoras im Dreieck KCB: r² = a² + b² = ³⁄₂a² (2)

Cosinussatz im Dreieck KSB: r² = b² + x² − 2bx cos 135°

Jetzt könnten wir b = ½a√2 und cos 135° = −½√2 einsetzen und kämen direkt zu (4), aber wir wollen ja keine Wurzeln.

Also anders: cos 135° = −cos (180° − 135°) = −cos 45°, somit r² = b² + x² + 2bx cos 45° (3)

Cosinussatz im Dreieck BAK, diesmal nicht für den rechten Winkel (Pythagoras ist ja ein Spezialfall des Cosinussatzes), sondern für einen der anderen: b² = a² + b² − 2ab cos 45°, somit a² = 2ab cos 45°, also 2b cos 45° = a

Das in (3) eingesetzt: r² = b² + x² + ax (4); mit (1) und (2): ³⁄₂a² = ½a² + x² + ax, also a² = x² + ax

Geteilt durch ax ergibt: a : x = (x + a) : a. Da isser, der goldene Schnitt.

LLAP 🖖