Mathematik zum Monatsende

[Rolf b]

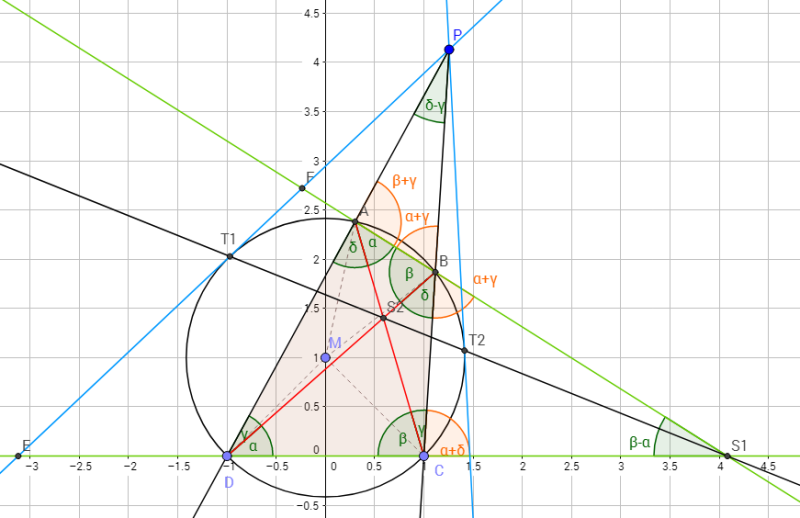
Ich habe mal einiges an Winkel- und Verhältnisforschung betrieben. Meine Darstellung habe ich "normalisiert", indem ich C und D auf (1,0) und (-1,0) festgesetzt habe und M auf die Y-Achse beschränkt. Variation gibt es nur noch durch Verschieben von M und P. OBDA gehe ich auch davon aus, dass P im 1. Quadranten liegt (bei anderer Lage müsste ich die von Geogebra gemalten Winkel anders definieren).

Über Sehnenvierecke habe ich gelernt, dass die Winkel zwischen den Rändern und den Diagonalen ein paar nette Eigenschaften haben. Jeweils 2 sind gleich (weil Peripheriewinkel zur gegenüberliegenden Seite), und die vier vorkommenden Werte addieren sich zu 180° (man betrachte die Verteilung der Winkel und z.B. die Dreiecke ACB und DCA).

Die orangefarbenen Winkel ergeben sich als Nebenwinkel, und wenn man $$\alpha+\beta+\gamma+\delta=180^\circ $$ ausnutzt, findet man $$\delta-\gamma$$ und $$\beta-\alpha$$ als Werte für die Winkel bei P und S1.

Auf Grund der Winkelverteilung ergibt sich auch, dass die sich gegenüberliegenden Dreiecke, die von den Diagonalen gebildet werden, ähnlich sind.

Durch Anwendung des Sekantensatzes ergeben sich ein paar interessante Verhältnisse:

$$\frac{\overline{DS_1}}{\overline{AS_1}} = \frac{\overline{BS_1}}{\overline{CS_1}} \ \mathrm{und}\ \frac{\overline{BP}}{\overline{AP}} = \frac{\overline{DP}}{\overline{CP}}$$

Und es gibt noch zwei wichtige Ähnlichkeiten, auf Grund von Winkelübereinstimmungen: $$\triangle DBP \sim \triangle CAP$$ und $$\triangle DS_1B \sim \triangle CS_1A$$. Aus diesen Ähnlichkeiten folgt:

$$\frac{\overline{DS_1}}{\overline{AS_1}} = \frac{\overline{BD}}{\overline{AC}} = \frac{\overline{DP}}{\overline{CP}}$$

und DAS ist nun total geil, weil wir damit eine Relation zwischen den Seitenlängen der Dreiecke haben, die durch die Sekanten gebildet werden.

Aus dem Sekanten-Tangenten-Winkelsatz folgt dann noch $$\overline{T_1P}^2 = \overline{DP}\cdot\overline{AP} = \overline{CP}\cdot\overline{BP}$$

Das ist alles schön und gut, aber ob das zur Problemlösung beiträgt, habe ich noch nicht entdeckt. Vielleicht ist ja für einen von euch was dabei, was hilft.

Rolf