Mathematik zum Monatsende - Beweis für einen Spezialfall
bearbeitet vonHallo Matthias Apsel,
Einen Beweis, wenn eine Sehne Durchmesser ist:
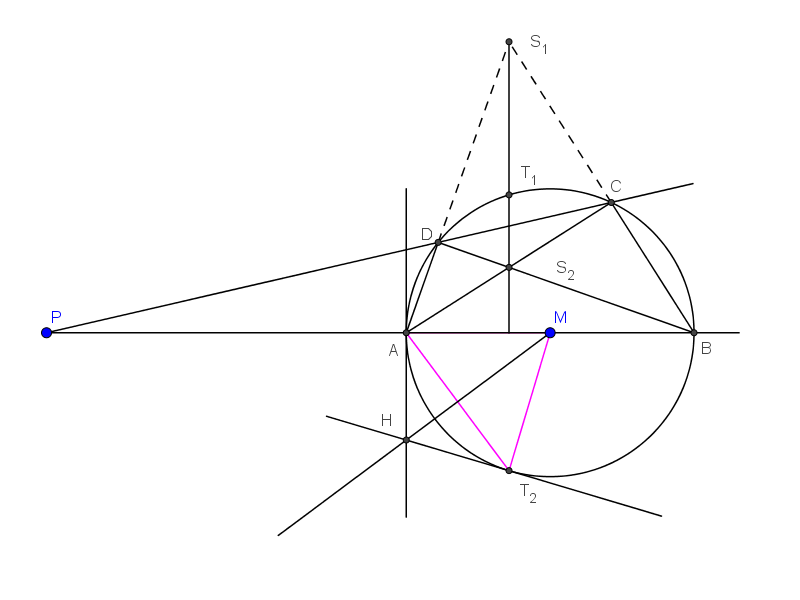
Die Peripheriewinkel bei _C_ und _D_ sind rechte Winkel (Satz des Thales), damit sind die Diagonalen Höhen im Dreieck _ABS₁_.
_S₂_ ist also das Orthozentrum dieses Dreiecks.
Damit steht die Gerade, auf der die Punkte _S₁_, _S₂_, _T₁_ und _T₂_ liegen, senkrecht auf _AB_. (sie ist die dritte Höhe)
Wegen der Symmetrie ist das Dreieck _PT₁T₂_ gleichschenklig. Das ist schon mal ein gutes Zeichen dafür, dass _T₁_ und _T₂_ tatsächlich die Berührungspunkte sind.
[](/images/e465038b-d147-40a6-acee-091a09c3ad53.png)
Weiter im Text.
Das Dreieck _T₂MA_ ist gleichschenklig. In _A_ wird die Senkrechte errichtet, der Winkel bei _M_ wird halbiert. Es entstehen die kongruenten Dreiecke _HMA_ und _MHT₂_. (sie haben die Seite _MH_ gemeinsam, eine weitere Strecke ist der Radius des Kreises, zudem ist der Winkel bei _M_ halbiert worden, Kongruenzsatz SWS)
Damit ist der Winkel bei _T₂_ ebenfalls ein rechter und _T₂_ somit Berührungspunkt der Tangente.
Wegen der Gleichschenkligkeit von _PT₁T₂_ ist auch _T₁_ Berührungspunkt der zweiten Tangente.
Bis demnächst
Matthias
--
Rosen sind rot.


