Mathematik zum Herbstanfang - Lösung

[Gunnar Bittersmann]

@@Matthias Apsel

@Gunnar Bittersmann legt ein reguläres Tetraeder in den Koordinatenursprung und streckt dieses um den passenden Faktor in y-Richtung. Clever.

Und so geht’s: Der Tetraeder ABCD hat die Kantenlängen AD = BC = 2. (AB = AC = DB = DC = √6, spielt aber keine Rolle.)

Anstelle des Volumens von ABCD berechne ich das Volumen eines regulären Tetraeders der Kantenlänge 2; das beträgt ⅔√2.

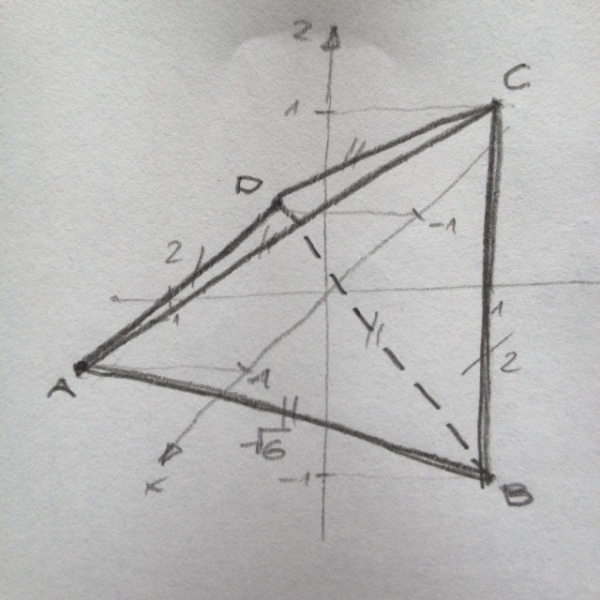
Ich lege einen regulären Tetraeder EFGH der Kantenlänge 2 so, dass sein Mittelpunkt in O liegt und dass EH ∥ AD und FG ∥ BC. Die Koordinaten seiner Eckpunkte sind:
E(1, −s, 0),
F(0, s, −1),
G(0, s, 1),
H(−1, −s, 0). mit 0 < s < 1.^[1]

Wir berechnen die Kantenlängen^[2]: EF = EG = HF = HG = √(4s² + 2); EH = FG = 2. Nun soll √(4s² + 2) = 2 sein; also s = ½√2.

Um von s auf 1 zu kommen, muss man mit √2 multiplizieren; g.h. um von EFGH zu ABCD zu kommen, muss man um den Faktor √2 in y-Richtung strecken.

Damit vergrößert sich das Volumen um ebendiesen Faktor; das Volumen von ABCD ist also √2 · ⅔√2 = ⁴⁄₃.

LLAP 🖖

---

1. Er könnte auch an der xz-Ebene gespiegelt liegen; wir wählen diesen. ↩︎

2. Der Abstand d zweier Punkte errechnet sich aus d² = (x₁ − x₂)² + (y₁ − y₂)² + (z₁ − z₂)². ↩︎