Mathematik zum Wochenanfang

[Gunnar Bittersmann]

… oder zum verlängerten Wochenende.

(Aufgabe von Antonio Gutierrez, gogeometry.com)

Kreis mit Radius r
darauf Punkte A, B, C, D, E derart, dass:
∠ABC = 45°
AB ∥ CD
BC ∥ DE
AB = a, BC = b, CD = c, DE = d

Zu zeigen: a² + c² = b² + d² = 4r²

LLAP 🖖

[Rolf B]

Hallo Gunnar,

a²+c² = r² ist falsch

Richtig ist a²+c² = 4r². Das ist relativ schnell ermittelt. An b und d muss ich noch etwas grübeln.

Rolf

[Gunnar Bittersmann]

@@Rolf B

a²+c² = r² ist falsch

Richtig ist a²+c² = 4r².

Womit du recht hast. Tippfehler im OP berichtigt.

LLAP 🖖

[ottogal]

Vorbemerkung:

Das Folgende hat nur Sinn, wenn [AB] bzw. [BC] nicht durch den Kreismittelpunkt geht, da dann die Sehne [CD] bzw. [DE] nicht existiert - C fällt mit D bzw. D fällt mit E zusammen; die Parallele würde jeweils zur Tangenten.

Die Mittelsenkrechte einer Sehne geht durch den Kreismittelpunkt.
Die parallelen Sehnen [AB] und [CD] haben die gemeinsame Mittelsenkrechte FG.
Die grünen Dreiecke AMF und CMG sind also rechtwinklig mit jeweils einem Kreisradius als Hypotenuse.

Der zum Umfangswinkel <ABC=45° gehörende Mittelpunktswinkel ist doppelt so groß: <AMC=90°. Also ergänzen sich die Winkel <FMA und <GMC ebenfalls zu 90°.

Daher stimmen die grünen Dreiecke AMF und CMG außer in der Hypotenuse r auch in den spitzen Winkeln überein und sind folglich kongruent.

Die Katheten haben somit die Längen |AF|=|MG|=a/2 und |MF|=|CG|=c/2.
Nach Pythagoras ist (a/2)²+(c/2)²=r² und damit a²+c²=4r².

Durch eine analoge Überlegung mit der Mittelsenkrechten HK, dem Mittelpunktswinkel <DMB und den violetten Dreiecken BMH und DMK erhält man die zweite Aussage b²+d²=4r².

[ottogal]

Vorbemerkung:

Das Folgende hat nur Sinn, wenn [AB] bzw. [BC] nicht durch den Kreismittelpunkt geht, da dann die Sehne [CD] bzw. [DE] nicht existiert - C fällt mit D bzw. D fällt mit E zusammen; die Parallele würde jeweils zur Tangenten.

Die Mittelsenkrechte einer Sehne geht durch den Kreismittelpunkt.

B und E sind Spiegelbilder von C bzw. D an der Achse HK, der Mittelsenkrechten von [BC]. Deshalb ist |BE|=|CD|=c.

Der Winkel <CBE ist als Spiegelbild des Winkels <BCD so groß wie dieser; der hat aber 45° (als Z-Winkel zu <ABC, da CD//AB).

Also ist <ABE=90°, und nach der Umkehrung des Thalessatzes ist folglich [AE] ein Kreisdurchmesser. Pythagoras in Dreieck AEB liefert dann a²+c²=4r².

A und D sind Spiegelbilder von B bzw. C an der Achse FG, der Mittelsenkrechten von [AB]. Deshalb ist |AD|=|BC|=b.

Da [AE] Kreisdurchmesser ist, ist Dreieck EAD nach Thales rechtwinklig, und Pythagoras liefert b²+d²=4r².

[Rolf B]

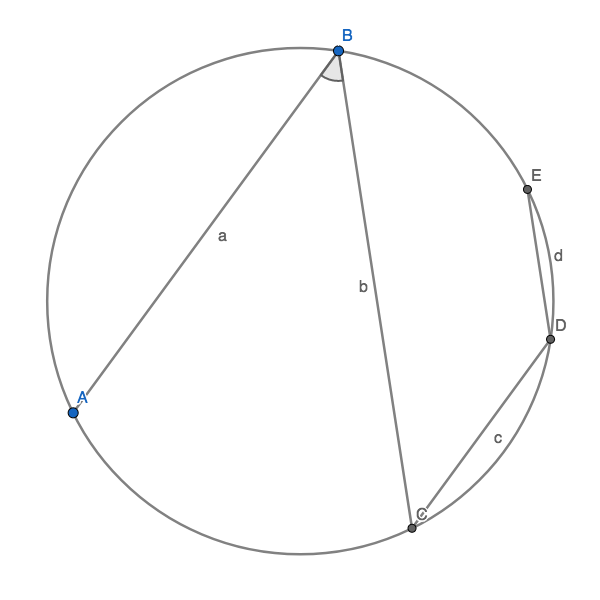
Meine Lösung ist Ottogals zweiter Lösung ähnlich. Sie ist allerdings genauso wie Ottogals Lösungen unvollständig; vermutlich verläuft die Argumentation in den beiden anderen Fällen ähnlich, aber ich hatte bisher keine Zeit dafür.

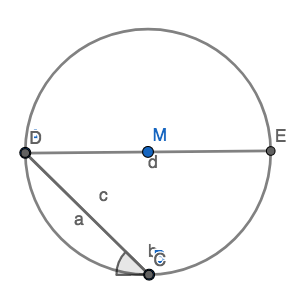
Der von Ottogal ausgeschlossene Fall, dass a durch M geht, ist relativ einfach zu behandeln. a ist in dem Fall 2r, C und D fallen zu einem Punkt zusammen, d.h. c ist 0, also a²+c²=4r². b wird zur Strecke BD und hat, wie gleich gezeigt wird, die Länge $$\sqrt2 r$$. d fällt dann mit b zusammen, damit ist b²+d² ebenfalls 4r².

Der Fall, dass b durch M geht, ist ähnlich. Das rote Trapez wird zum Quadrat, a und c haben eine Länge von $$\sqrt2 r$$. b hat die Länge 2r, D und E fallen zu einem Punkt zusammen, d.h. d hat die Länge 0. Es gelten äquivalente Rechnungen zum vorigen Fall.

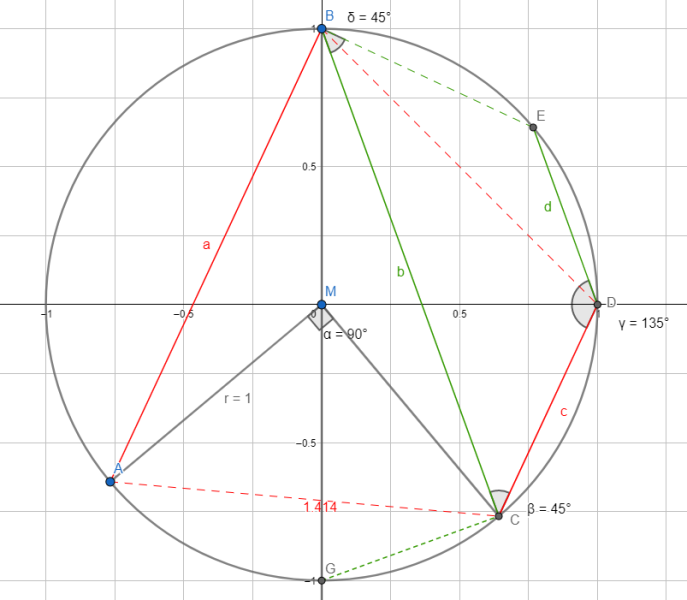
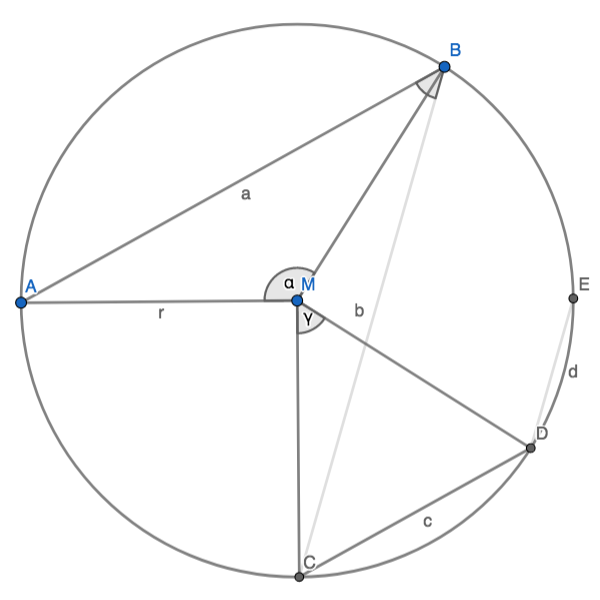
∢ABE hat nach Aufgabenstellung 45°, d.h. ∢AMC beträgt nach Zentriwinkelsatz 90°. Damit ist die Länge von AC berechenbar, es ist $$\sqrt2 r$$.

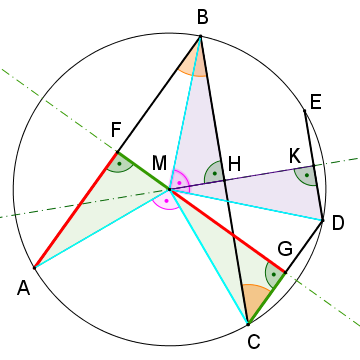
G sei der Punkt, der B auf dem Kreis gegenüberliegt (also der Schnittpunkt von BM mit dem Kreis).

Das rote Trapez (wie auch das grüne) sind symmetrisch. Ihre parallelen Seiten sind Sehnen des Kreises, d.h. ihre Mittelsenkrechten laufen beide durch M, und weil die Seiten parallel sind, sind die Mittelsenkrechten identisch.

Aus den Symmetrien folgt mehreres:

• Es ist $$\overline{BD}=\overline{AC}$$ (rotes Trapez), deswegen sind ΔACM und ΔDBM sss-kongruent und ∢DMB beträgt 90°, d.h. D halbiert den Kreisumfang von D nach G. Die Lage von D ist unabhängig von der Lage von A!
• $$\overline{BE}=\overline{CD}$$ (Symmetrie des grünen Trapezes)
• ∢CBE beträgt 45°, d.h. ∢ABE hat 90°. ΔAEB ist rechtwinklig, demzufolge bildet der Kreis einen Thaleskreis über AE, und nach Pythagoras ist a²+c²=4r²

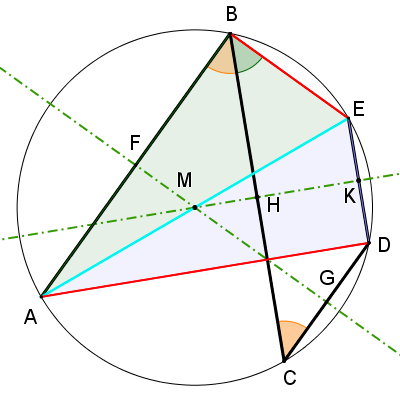
Weil die Lage von D fix ist, D den Umfang von B nach G halbiert, und die Längen von CD und BE gleich sind, sind auch die Längen von DE und GC gleich. ΔBGC liegt unter einem Thaleskreis, bei C hat es also einen rechten Winkel und daraus folgt auch b²+d²=4r²

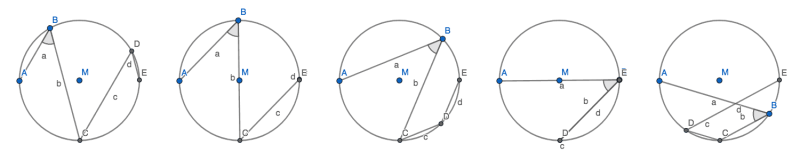
Die Zeichnung gilt für den Fall, den Gunnars Aufgabenbild zeigt, d.h. A liegt im Quadranten III. Liegt A im Quadranten II oder IV, sind $$\scriptstyle{\vec{BC}}$$ und $$\scriptstyle{\vec{ED}}$$ nicht mehr gleich orientiert und die Argumentation dürfte anders verlaufen, das sind zwei Fälle die ich noch betrachten muss. Liegt A im Quadranten I, funktioniert die Konstruktion nicht, weil C dann nicht mehr auf dem Kreis liegend konstruierbar ist.

Rolf

[ottogal]

Hallo Rolf,

Der von Ottogal ausgeschlossene Fall, dass a durch M geht, ist relativ einfach zu behandeln.

Es ist zwar interesssant, dass die zu beweisenden Formeln auch für die Sonderfälle c=0 bzw. d=0 gelten. Ich denke aber, dass sie für die Aufgabenstellung nicht behandelt werden müssen, da für sie ja die Bedingung CD//AB bzw. DE//CB sinnfrei ist.

G sei der Punkt, der B auf dem Kreis gegenüberliegt (also der Schnittpunkt von BM mit dem Kreis).

D halbiert den Kreisumfang von D nach G.

Du meinst: D halbiert den Kreisbogen von B nach G.
(Kreisumfang ist $$2 \pi r$$)

Gut gesehen, dass CD und BE gleich lang sind und so das ΔBGC zu verwenden ist.

Liegt A im Quadranten I, funktioniert die Konstruktion nicht, weil C dann nicht mehr auf dem Kreis liegend konstruierbar ist.

Mein GeoGebra-Blatt dazu verhält sich dann ganz chaotisch. 😀

Viele Grüße
ottogal

[Gunnar Bittersmann]

@@ottogal

Es ist zwar interesssant, dass die zu beweisenden Formeln auch für die Sonderfälle c=0 bzw. d=0 gelten. Ich denke aber, dass sie für die Aufgabenstellung nicht behandelt werden müssen, da für sie ja die Bedingung CD//AB bzw. DE//CB sinnfrei ist.

Ist sie das?

Na gut, vielleicht hätte man die Aufgabe anders formulieren sollen. Anstatt AB ∥ CD: Der (andere) Schnittpunkt der Parallelen zu AB durch C mit dem Kreis sei D. Dann kann die Parallele zu AB durch C durchaus Tangente sein und D ≡ C. Für BC ∥ DE analog.

LLAP 🖖

[ottogal]

Na gut, vielleicht hätte man die Aufgabe anders formulieren sollen.

Ja dann ...

[Gunnar Bittersmann]

@@Gunnar Bittersmann

A͡B sei der Kreisbogen AB, auf dem C nicht liegt. 2πr ist Länge des Vollkreises, ¼ × 2πr also ein Viertelkreis, ½ × 2πr ein Halbkreis.

Für die Lage von A, B, C, D, E gibt es 5 Fälle:

1. A͡B < ¼ × 2πr, d.h. ∠AMB < 1∟
   Der Streckenzug ABCDE bildet ein M.

2. A͡B = ¼ × 2πr, d.h. ∠AMB = 1∟
   D und E fallen zusammen; d = 0.

3. ¼ × 2πr < A͡B < ½ × 2πr, d.h. 1∟ < ∠AMB < 2∟
   Der Streckenzug ABCDE bildet ein S bzw. Ƨ.

4. A͡B = ½ × 2πr, d.h. ∠AMB = 2∟
   C und D sowie B und E fallen zusammen; c = 0.

5. ½ × 2πr < A͡B < ¾ × 2πr, d.h. 2∟ < ∠AMB < 3∟
   Der Streckenzug ABCDE bildet ein ɣ.

Die beiden Fälle, in denen eine der Sehnen zu einem Punkt entartet, sind schnell besprochen:

In Fall 2 ist ∠AMB = 1∟ und ∠AMC = 1∟, ∠BMC als Summe der beiden also ein gestreckter Winkel, d.h. BC ist Durchmesser. Aus b = 2r folgt b² + d² = 4r² wegen d = 0.

Aus ∠ABC = ∠BCD (Wechselwinkel an geschnittenen Parallelen folgt a = c. Pythagoras in △ABC: a² + a² = b², also a² + c² = 4r².

In Fall 4 ist AB Durchmesser. Aus a = 2r folgt a² + c² = 4r² wegen c = 0.

C ≡ D liegt auf dem Thaleskreis, △ABC ist gleichschenlig-rechtwinklig mit Kathetenlänge b = d. Pythagoras in △ABC: b² + d² = a² = 4r².

LLAP 🖖

[Gunnar Bittersmann]

@@Gunnar Bittersmann

A͡B sei der Kreisbogen AB, auf dem C nicht liegt. 2πr ist Länge des Vollkreises, ¼ × 2πr also ein Viertelkreis, ½ × 2πr ein Halbkreis.

Für die Lage von A, B, C, D, E gibt es 5 Fälle:

Oder doch 6:

6. A͡B = ¾ × 2πr, d.h. ∠AMB = 3∟
   B und C sowie A und D fallen zusammen; b = 0.

In dem Fall ist AE Durchmesser. Aus d = 2r folgt d² + b² = 4r² wegen b = 0.

∠BAE = 45° (Wechselwinkel zum Winkel zwischen AB und der Tangenten) B ≡ C liegt auf dem Thaleskreis, △ABE ist gleichschenlig-rechtwinklig mit Kathetenlänge a = c. Pythagoras in △ABE: a² + c² = d² = 4r².

Noch größer als ¾ × 2πr darf A͡B nun aber wirklich nicht sein.

LLAP 🖖

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Ich hatte es auch so wie ottogals zweite Lösung. Naja, jedenfalls auf dem Papier für b und d. Mir war klar, dass das für die andere Mittelsenkrechte auch für a und c gilt; ich hätte nur noch mal genau hinkucken und das aufschreiben müssen.

Ich hab noch einen anderen Lösungsansatz für die Fälle 1 bis 3 sowie Fall 5:

∠AMC = ∠BMD = 1∟ hatten wir ja schon.

α = ∠AMB, γ = ∠CMD; α + γ = π

Cosinussatz in △ABM: (1) a² = 2r² − 4r² cos α

und in △CDM: (2) c² = 2r² − 4r² cos γ = 2r² − 4r² cos(π − α) = 2r² + 4r² cos α

(1) + (2) ergibt a² + c² = 4r²

Das lässt sich auf diesem Weg sicher auch für b und d zeigen.

LLAP 🖖

[Rolf B]

Hallo Gunnar,

Cosinussatz⁉️

Und da heißt es, ich denke kompliziert...

Aber zwischendurch war ich da auch mal 😂 – bis ich mir dann vorstellte, von euch irgendeine simple Strahlensatzlösung um die Ohren gehauen zu bekommen, und nochmal hingeguckt habe.

Schöne Aufgabe, jedenfalls.

Rolf

[ottogal]

In diesem Thread gut zu beobachten:

Eine eingefügte Bilddatei (z.B. im PNG-Format) wird erheblich größer dargestellt als das Original; verkleinert man sie vorsorglich vorher, wird sie unscharf.
(Firefox, Windows 10, 1920x1080)

Warum ist das so? Kann man das nicht ändern?

[Rolf B]

Hallo ottogal,

ich habe den Effekt eigentlich nicht, eher im Gegenteil: Zu breite Bilder werden verkleinert. Das liegt am Foren-CSS, da steht max-width:100% für Bilder im Text.

Wenn ich ein „zu kleines“ Bild hochlade, bleibt es in seiner Größe.

Was mir auffällt, ist der Queryparameter ?size=medium an den Bilder-URLs. Andere Werte als medium, die einen erkennbaren Effekt auslösen würden, habe ich nicht gefunden (müsste wohl im Git rumturnen um zu schauen was da passiert...).

Hast Du vielleicht ein User-CSS drin? Oder im Brauser eine Skalierung aktiviert?

Rolf

[ottogal]

Was mir auffällt, ist der Queryparameter ?size=medium an den Bilder-URLs.

Das ist mir auch aufgefallen. Wäre gut zu wissen, ob man an der Stelle drehen kann.

Hast Du vielleicht ein User-CSS drin? Oder im Brauser eine Skalierung aktiviert?

Ein User-CSS verwende ich nicht. Aber ich skaliere auf 120%, um die Texte vernünftig lesen zu können. Die Bilder erscheinen etwa in Originalgröße, wenn ich auf 80% herunterskaliere. Dann werden die Texte aber ermüdend klein.

Inzwischen habe ich mir das in der Firefox Developer Edition angesehen: Dort ist die Diskrepanz viel geringer. Scheint also eine Schwäche des regulären Firefox zu sein (59.03 (64 bit)).

Vielleicht ist es ein Problem von virtuellen vs. physischen Pixeln?

[ottogal]

Übrigens zeigt der normale Firefox (erst seit den letzten paar Updates) auch eine fehlerhafte Darstellung von TeX-Formeln.

Screenshots jeweils bei Skalierung 100%:

Firefox:

Firefox Developer Edition:

Ich werde wohl ganz auf die Dev-Edition umsteigen...

[Rolf B]

Hallo ottogal,

very merkwürdig. Bist Du sicher, dass Du da nicht irgendwelche differierenden Einstellungen hast?

Rolf

[Gunnar Bittersmann]

@@ottogal

Übrigens zeigt der normale Firefox (erst seit den letzten paar Updates) auch eine fehlerhafte Darstellung von TeX-Formeln.

Kann ich auf dem Mac nicht bestätigen.

Und SISO-Prinzip. Für Klammern sind \left( und \right) zu verwenden.

LLAP 🖖

[Matthias Apsel]

Hallo ottogal,

Firefox:

$$y=\sqrt{\frac{1}{4} - \left( x - \frac{1}{2} \right)^2}$$

$$y=\sqrt{\frac{1}{4} - ( x - \frac{1}{2} )^2}$$

Firefox Developer Edition:

In meinem FF 59.0.3 unter Win10 sieht es auch mit den falschen Klammern so aus, wie bei dir in der Entwicklerversion.

Bis demnächst
Matthias

[ottogal]

Hallo Matthias,

das freut mich für dich (ernsthaft).

Ich bin mir sicher, dass die Darstellung bei meinem Firefox bis vor wenigen Monaten korrekt war - auch bei TeX-Passagen in älteren Postings, die früher richtig, später eben verstümmelt angezeigt wurden. Daher ja meine Vermutung, dass eines der späteren Upgrades hier etwas kaputt gemacht hat.

Mir ist jedenfalls nicht erinnerlich, dass ich irgend eine andere Einstellung im Firefox geändert hätte (sei es Plugins oder Sonstiges).

Es bleibt mir rätselhaft...

[Matthias Apsel]

Hallo Rolf B,

Was mir auffällt, ist der Queryparameter ?size=medium an den Bilder-URLs. Andere Werte als medium, die einen erkennbaren Effekt auslösen würden, habe ich nicht gefunden (müsste wohl im Git rumturnen um zu schauen was da passiert...).

die gibt es i²rc auch nicht. medium ist ein auf 800 × 600 verkleinertes Bild, damit nicht 4000 × 3000 große Screenshots in die Beitragsansicht geladen werden, nur um verkleinert dargestellt zu werden. Außerdem gibt es noch thumb.

Bis demnächst
Matthias