Mathematik zum Wochenanfang - Meine erste Lösung

[ottogal]

Vorbemerkung:

Das Folgende hat nur Sinn, wenn [AB] bzw. [BC] nicht durch den Kreismittelpunkt geht, da dann die Sehne [CD] bzw. [DE] nicht existiert - C fällt mit D bzw. D fällt mit E zusammen; die Parallele würde jeweils zur Tangenten.

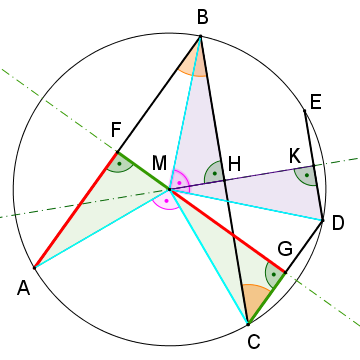
Die Mittelsenkrechte einer Sehne geht durch den Kreismittelpunkt.
Die parallelen Sehnen [AB] und [CD] haben die gemeinsame Mittelsenkrechte FG.
Die grünen Dreiecke AMF und CMG sind also rechtwinklig mit jeweils einem Kreisradius als Hypotenuse.

Der zum Umfangswinkel <ABC=45° gehörende Mittelpunktswinkel ist doppelt so groß: <AMC=90°. Also ergänzen sich die Winkel <FMA und <GMC ebenfalls zu 90°.

Daher stimmen die grünen Dreiecke AMF und CMG außer in der Hypotenuse r auch in den spitzen Winkeln überein und sind folglich kongruent.

Die Katheten haben somit die Längen |AF|=|MG|=a/2 und |MF|=|CG|=c/2.
Nach Pythagoras ist (a/2)²+(c/2)²=r² und damit a²+c²=4r².

Durch eine analoge Überlegung mit der Mittelsenkrechten HK, dem Mittelpunktswinkel <DMB und den violetten Dreiecken BMH und DMK erhält man die zweite Aussage b²+d²=4r².