@@Gunnar Bittersmann
@m. lag nicht allzuweit weg, alle anderen auf der faulen Haut‽ (Zeugma; Heinz Erhardt wäre begeistert.)
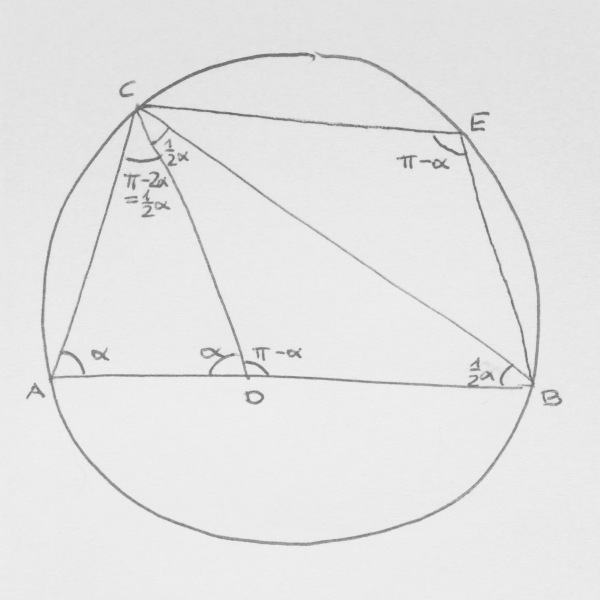
Alle 4 Dreiecke sind gleichschenklig.
War die Schwierigkeit, dass vierte Dreieck zu finden? In der Zeichnung: △ABC. Es war keine Rede davon, dass die Schenkel aller Dreiecke gleich lang wären. AB = CB; wie man leicht sieht, sind es diese beiden Seiten in △ABC, die gleich lang sind.
Sei α = ∠BAC. Aus der Gleichschenkligkeit von △ADC folgt ∠CDA = α. Wegen Innenwinkelsumme ist ∠ACD = π − 2α.
∠BDC = π − α. Wegen Gleichschenkligkeit von △DBC und Innenwinkelsumme ist ∠DCB = ∠CBD = ½α.
Aus der Gleichschenkligkeit von △ABC folgt ∠ACB = ∠BAC = α. Damit ist ∠ACD = α − ½α = ½α.
½α = π − 2α
⁵⁄₂α = π
α = ⅖π
∠BAC und ∠CEB sind gegenüberliegende Winkel im Sehnenviereck, ergänzen sich also zu π. Damit ist der gesuchte Winkel ∠CEB = π − α = ⅗π.
Manche mögen’s heiß: ⅗π sind 108°.
Mögt Ihr eigentlich noch Mathematik zum … oder hat sich das totgelaufen?
LLAP 🖖
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann