nicht angemeldet
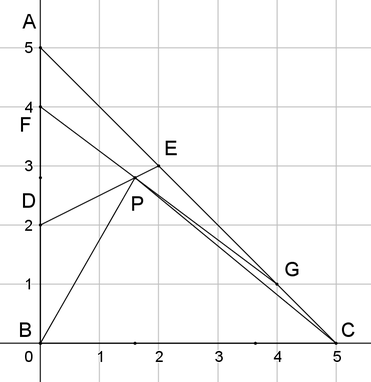
Am Verhältnis der Strecken und der Flächeninhalte ändert sich nichts, wenn man die Ecken von Dreick ABC so in ein kartesisches Koordinatensystem legt, dass A(0;5), B(0;0) und C(5;0) ist:
Dann ist D(0;2), E(2/3), F(0;4) und G(4;1).
Die Gerade DE hat die Gleichung $$y=\frac{1}{2}x+2$$;
die Gerade FG hat die Gleichung $$y=-\frac{3}{4}x+4$$;
Die x-Koordinate des Schnittpunkts P von DE mit FG muss also die Gleichung
$$\frac{1}{2}x+2=-\frac{3}{4}x+4$$
erfüllen. Man erhält $$x=\frac{8}{5}$$ und damit $$y=\frac{14}{5}$$.
Die Flächeninhalte der Dreiecke BCP und BCA verhalten sich wie ihre Höhen, da sie in der Grundseite |BC| übereinstimmen. Somit ist das gesuchte Flächenverhältnis $$\frac{14}{5}:5$$, also $$\frac{14}{25}$$ oder 56%.
Gunnar Bittersmann
Matthias Apsel