nicht angemeldet
Gunnar Bittersmann@@Gunnar Bittersmann
Mich erreichten zwei Lösungen; beide hatten die Sekante AD und die Tangente in F bis zu ihrem Schnittpunkt verlängert. Aber wozu in die Ferne schweifen …?
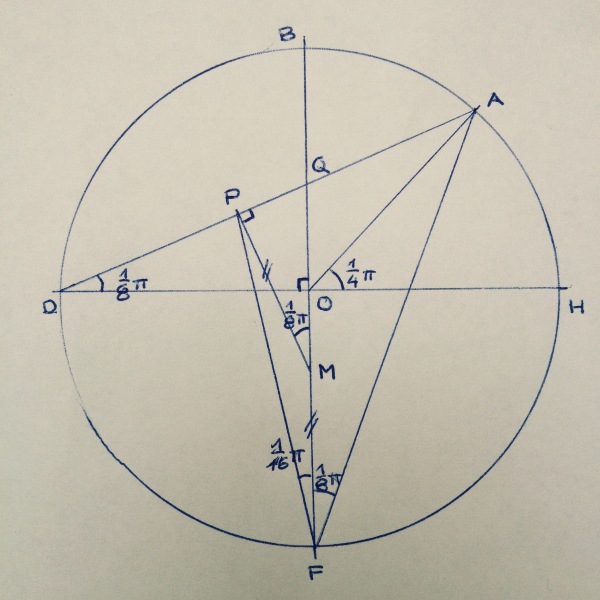
O Mittelpunkt des Kreises O₁; M Mittelpunkt des Kreises O₂; Q Schnittpunkt von AD und OB.
Damit sich die beiden Kreise in F berühren (sie also in F eine gemeinsame Tangente haben), muss M auf OF liegen.
∠HOA = ½∟ = ¼π.
Der zu diesem Zentriwinkel gehörige Peripheriewinkel ist halb so groß: ∠HDA ≡ ∠ODQ = ⅛π.
Die Dreiecke DOQ und MPQ stimmen im Winkel ∠DQO ≡ ∠PQM sowie im rechten Winkel überein, damit ist ∠QMP = ⅛π.
Ebenso groß ist auch die Summe ∠FPM + ∠MFP = ⅛π. Wegen MP = MF (Radien des Kreises O₂) sind beide Winkel gleich groß, also ∠MFP = ⅟₁₆π.
∠AFB = ∠HDA = ⅛π.
∠AFP = ∠AFB + ∠MFP = ³⁄₁₆π.
LLAP 🖖
“When UX doesn’t consider all users, shouldn’t it be known as ‘Some User Experience’ or... SUX? #a11y” —Billy Gregory