Mathematik zum Wochenende

[Rolf B]

Ich werfe mal einen Haufen unausgegorenes in die Runde… (Geogebra Link)

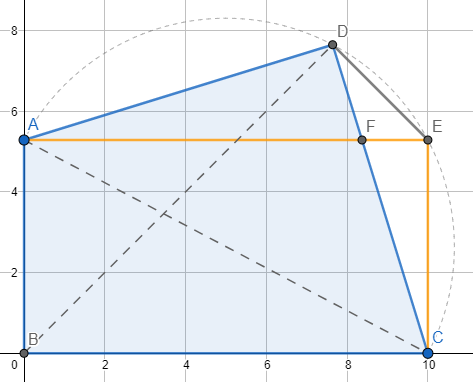
Wenn man den Punkt E hinzufügt, erhält man zwei Dreiecke FCE und AFD^[1]. Die sind ähnlich, und es ist so, dass sich die Fläche von ABCD aus (ABCE - FCE + AFD) errechnet. Ähnlich sind auch FED und BDA (folgt aus der Ähnlichkeit von FCE und AED).

Der Winkel CBD ist 45°, egal wo A liegt. Wenn ich A auf der y-Achse verschiebe, bewegt sich D, aber immer nur auf der 1. Winkelhalbierenden. Dafür gibt's sicher einen Beweis, ich habe ihn nur noch nicht.

Wenn man das Größenverhältnis der ähnlichen Dreiecke aus der y-Koordinate von A ableiten könnte, wäre das vielleicht ein Weg. Bisher habe ich noch keine Idee dazu.

Rolf

---

1. Korrigiert nach Hinweis durch Tabellenkalk ↩︎