Ellipsen überfordern mich - bitte um Hilfe

[ottogal]

Hallo Felix, hallo in die Runde,

das Folgende ist wahrscheinlich eher nicht weiterführend für die ursprüngliche Fragestellung. Jedenfalls ist es eine interessante Beziehung für sich berührende Ellipsen, deshalb stelle ich es vor.

Bekanntlich (? 😉) gilt:

Die Normale in einem Ellipsenpunkt ist die Winkelhalbierende der Brennstrahlen zu diesem Punkt.

(Die "Normale" ist die zur Tangente senkrechte Gerade im Berührpunkt; "Brennstrahlen" nennt man die Verbindungsstrecken des Ellipsenpunkts mit den Brennpunkten.)

Siehe dazu z.B. Brennpunkteigenschaft bei Wikipedia.
"Anwendung" findet dies z.B. beim so gen. "Flüstergewölbe". Das ist ja auch für den Musiker von Interesse...

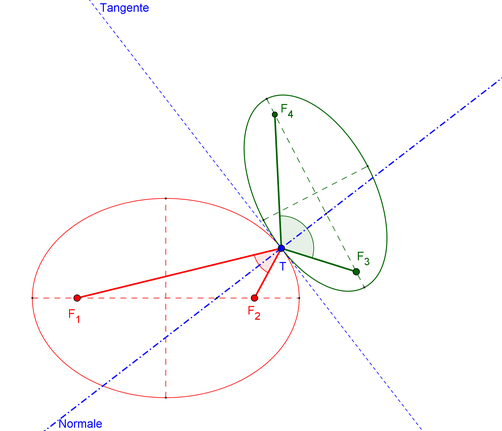
Berühren sich zwei Ellipsen in einem Punkt T, so haben sie in diesem die Tangente und daher auch die Normale gemeinsam.

Die Normale in T zur einen Ellipse muss daher auch in der anderen Ellipse den Winkel zwischen den Brennstrahlen zu T halbieren.

In meinem GeoGebra-Blatt "Tangentiale Ellipsen" sind der Punkt T und die Brennpunkte F1 und F2 der ersten sowie F3 und F4 der zweiten Ellipse verschiebbar; F4 ist jedoch in der Bewegung so eingeschränkt, dass der Winkel zwischen den Brennstrahlen von F4 und F3 ebenfalls von der Normalen halbiert wird.

Schaut mal rein...
Viele Grüße
ottogal