Hallo,
das Wochenende ist rum, dann poste ich mal was.
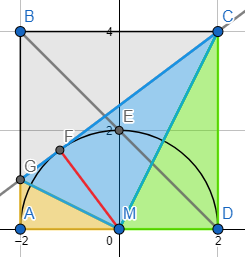
In diesem Beitrag sei r der Radius des Halbkreises. Das Quadrat hat damit eine Kantenlänge von 2r und eine Fläche von 4r².
#Teil 1
Das grüne, orange und blaue Dreieck sind zueinander ÄHNLICH.
Warum?
Sei α=FCD und δ=AGF. Die Vierecke AMFG und DCFM sind Drachen, wegen der Symmetrie von Tangenten an den jeweiligen Zentralen, deswegen ist <AMG=(90°-δ/2) und <CMD=(90°-α/2). Und weil α und δ Nachbarwinkel an parallelen Geraden sind, ergänzen sie sich zu 180°. Damit gilt:
$$\angle{AMG} + \angle{CMD} = 90^\circ-\frac{\delta}{2}+ 90^\circ-\frac{\alpha}{2} = 180^\circ-\frac{\alpha+\delta}{2}=90^\circ$$
und es bleiben für <GMC noch genau 90° übrig.
Und das heißt, dass das grüne und orange Dreieck jeweils zwei Winkel mit dem blauen Dreieck gemeinsam haben, und deswegen sind alle drei ähnlich.
Nebenbei ist noch $$\overline{AM} = \overline{MD} = r$$ und $$\overline{DC}=2r$$. Damit berechnet sich:
$$\frac{\overline{GA}}{\overline{AM}} = \frac{\overline{MD}}{\overline{CD}} \Longleftrightarrow \frac{\overline{GA}}{r} = \frac{r}{2r} \Longleftrightarrow \overline{GA}=\frac{r}{2}$$
Daraus berechnet sich $$\overline{BG} = \frac{3}{2}r$$ und wegen der Symmetrien an den Drachen ist $$\overline{GC} = \frac{r}{2}+2r = \frac{5}{2}r$$.
Das Verhältnis GB:BC:CG ist also 3:4:5. Überraschung :)
#Teil 2
Nach etlichem Gefummele bin ich auf die folgende Lösung gekommen. Tut mir leid, dass sie so lang geworden ist, für eine kürzere hatte ich keine Zeit 😉
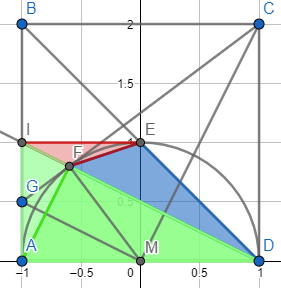
Ich möchte die Lage von I und F berechnen. Es scheint offensichtlich, dass I und E auf einer Höhe liegen, aber begründen muss man das schon.
Der Winkel GMC ist - wie bei Teil 1 gezeigt, ein Rechter. CM und FD stehen senkrecht aufeinander (weil Drachendiagonalen), ALSO sind MG und DI parallel. Deswegen ist auch $$\angle{AMG}=\angle{ADI}$$, die Dreiecke AMG und ADI sind demnach ähnlich, und deswegen ist
$$\frac{\overline{IA}}{\overline{AD}} = \frac{\overline{GA}}{\overline{AM}} = \frac{0{,}5r}{r}=\frac{1}{2}$$
Dass die Länge von GA 0,5r beträgt, habe ich in Teil 1 gezeigt. IA ist also halb so lang wie AD und hat die Länge r, womit gezeigt ist, dass I auf gleicher Höhe wie E liegt.
Die Fläche von ADI ist berechnet sich damit zu r² oder ein Viertel des Quadrats.
Nun betrachte ich das Innere von ADI. Der Winkel AFD ist - nomen est omen - ein Rechter, weil unter dem Thaleskreis; AF ist also die Höhe von ADI. Teilt man ein rechtwinkliges Dreieck entlang seiner Höhe, sind die Teildreiecke zueiander und zum Gesamtdreieck ähnlich[1].
Weil AFI und ADF ähnlich sind UND die Grundseite von AFI halb sol lang ist wie die Grundseite von ADF, beträgt die Fläche von AFI ein Viertel der Fläche von ADF, die Flächen verhalten sich 1:4, also hat ADF vier fünftel der Fläche von ADI, oder 0,8r². Daraus kann man die Höhe von ADF auf AD berechnen - bzw. die y-Koordinate von F: Weil die Grundseite AD die Länge 2r hat, muss die Höhe 0,8r sein.
Weil IE auf Höhe r liegt, ist demnach die Höhe des roten Dreiecks 0,2r, und seine Fläche beträgt 0,1r².
Das rote und blaue Dreieck haben zusammen eine Fläche von 0,5r² (Grundseite IE hat Länge r, die Höhe ist ebenfalls r). Ziehe ich das rote Dreieck ab, bleibt 0,4r² für das blaue Dreieck übrig. Das Quadrat hat 4r², d.h. das blaue Dreieck (bei Gunnar das purpurfarbene) hat ein Zehntel der Fläche des Quadrats.
Yippie!
Rolf
sumpsi - posui - clusi
Für Details siehe Beweis des Kathetensatzes. ↩︎