nicht angemeldet
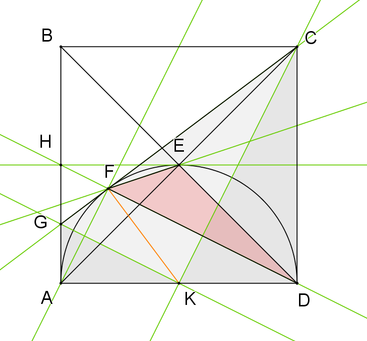
Ok, dann schreib ich auch mal meine Lösung auf:
O.b.d.A sei die Quadratseite 1. Der Kreismittelpunkt heiße K, der Schnittpunkt der Geraden DF mit der Strecke [AB] heiße H.
Die Tangentenabschnitte von C aus sind gleich lang, also ist CF=CD=1.
Die Winkelhalbierende von Winkel FCD steht senkrecht auf der Berührpunkt-Sehne FD und geht durch den kreismittelpunkt K.
Entsprechend steht die Winkelhalbierende von Winkel AGF senkrecht auf der Berührpunkt-Sehne AF und geht ebenfalls durch K.
Wegen des Satzes von Thales steht auch DF senkrecht auf AF. Somit sind GK und HD parallel.
Die Winkel KCD und HDA sind gleich, da sie paarweise orthogonale Schenkel haben. Somit sind die rechtwinkligen Dreiecke DCK und ADH kongruent, woraus folgt: AH = 1/2.
Der Strahlensatz liefert nun AG:AH = AK:AD = 1:2, mit AH = 1/2 folgt daraus FG = AG = 1/4.
Damit ist BG = 3/4, und mit FC = 1 erhält man CG = GF + FC = 5/4.
Da BC = 4/4 ist, folgt BG : BC : CG = 3 : 4 : 5.
Wegen gleicher Grundseite und Höhe haben die Dreiecke HED und HEA den gleichen Flächeninhalt; letzterer ist 1/8.
Wegen gleicher Höhe verhalten sich die Flächeninhalte von Dreieck FDE und Dreieck HDE wie die dazugehörigen Grundseiten, also
A(FDE) : A(HDE) = FD : HD = FC : GC = 1 : 5/4.
Man erhält A(FDE) = 1/8 : 5/4 = 1/10, also 10% der Quadratfläche.
Gunnar Bittersmann
Rolf B