@@ottogal
Dies als Zusatzaufgabe, wenn ihr mögt.
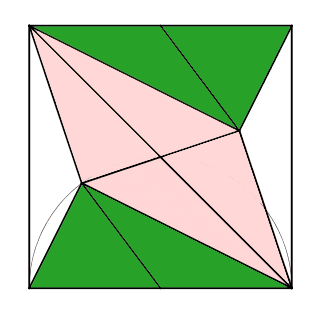
Die zweite Teilfrage (Flächenanteil des roten Dreiecks am Quadrat) kann man auch durch den Nachweis lösen, dass die folgende Zerlegung des Quadrats lauter flächengleiche Teildreiecke ergibt:
Irgendwann hatte ich die Lösung schon mal, aber gerade keine Zeit, sie vernünftig aufzuschreiben. Dann ist sie mir wieder entfleucht. Jetzt hab ich sie wieder.
Wegen Punktsymmetrie der Figur gilt:
- Die roten (hell schraffierten) Dreiecke bilden ein Paralleleogramm; die Diagonalen eines Parallelogramms teilen dieses in 4 gleichgroße Dreiecke.
- Die grünen (dunkel schraffierten) Dreiecke haben dieselbe Grundseitenlänge (halbe Seitenlänge des Quadrats) und dieselbe Höhe, sind also auch gleich groß.
- Die weißen Dreiecke sind auch untereinander gleich.
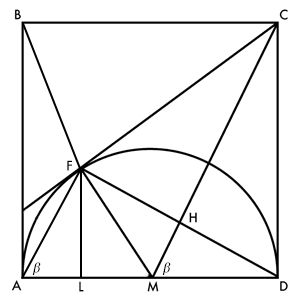
Bezeichnung der Punkte wie gehabt. L sei der Fußpunkt des Lotes von F auf AD.
Wegen △CFM ≅ △CDM steht FD senkrecht auf MC. Da auch ∡DFA ein rechter ist (Thales), ist ∡FAD = ∡HMD = β. Da die Dreiecke △ALF und △MDC außerdem im rechten Winkel übereinstimmen, sind sie ähnlich und es verhalten sich FL : AL = CD : MD = 2 : 1. FL und AL sind nun aber die Höhen in den Dreiecken △AMF und △ABF, deren Grundseiten sich wie 1 : 2 verhalten. Die Dreiecke sind also flächengleich, und damit auch alle grünen (dunkel schraffierten) und weißen Dreiecke.
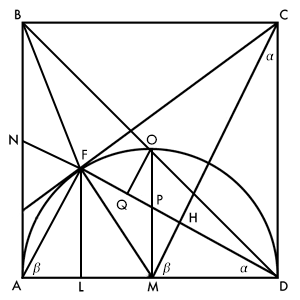
Sei O der Mittelpunkt des Quadrats. FD schneide AB in N und MO in P. Q sei der Fußpunkt des Lotes von O auf FD.
Wegen Innenwinkelsumme in den Dreiecken △CDM und △DFA ist ∡DCM = ∡ADF = α. Da die Dreiecke △MDC und △NAD außerdem im rechten Winkel und einer Seite (Seitenlänge des Quadrats) übereinstimmen, sind sie kongruent und es gilt MD = NA = NB (halbe Seitenlänge des Quadrats).
Nach Strahlensatz ist dann auch PM = PO. Da die Dreiecke △MPH und △OPQ außerdem im rechten Winkel und den Scheitelwinkeln übereinstimmen, sind sie kongruent und es gilt HM = QO. Das sind nun aber die Höhen in den Dreiecken △FDM und △FDO über derselben Grundseite FD. Die Dreiecke sind also flächengleich, und damit auch alle grünen (dunkel schraffierten) und roten (hell schraffierten) Dreiecke.
Damit sind alle 10 Dreiecke flächengleich, q.e.d.
„Aber wem erzähle ich das? Dem wissend zwinkernden? Wahrscheinlich doch nur dem Archiv.“ [at]
LLAP 🖖
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann