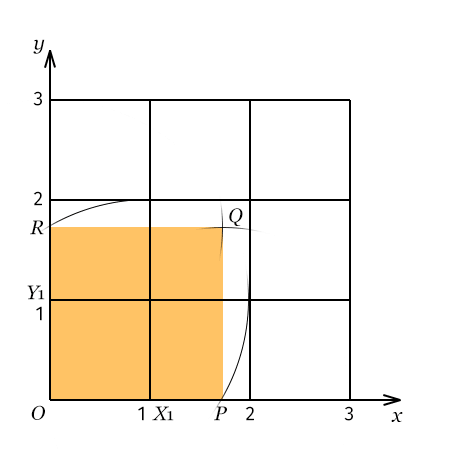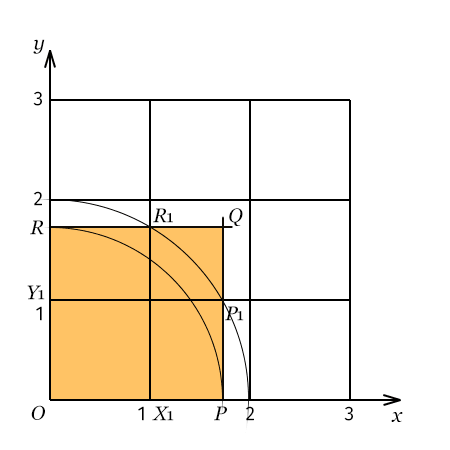Mathematik zum Wochenende – Lösungen

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Heute gibt’s mal nichts zu rechnen, sondern was zu malen:

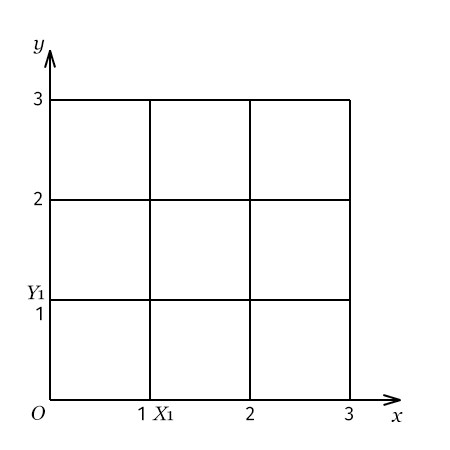
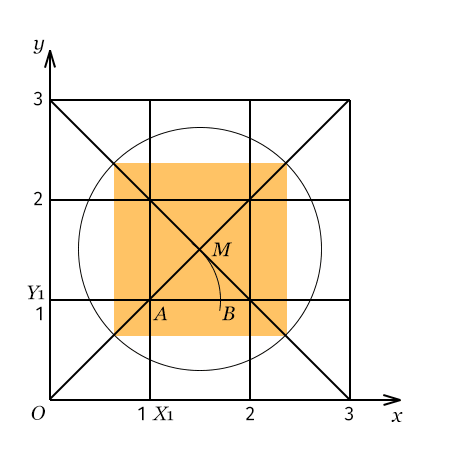
Damit wir wissen, worüber wir sprechen, male ich erstmal ein Koordinatensystem:

O(0,0) (O wie obviously), X₁(1, 0), Y₁(0, 1)

Konstruiere ein Quadrat der Fläche 3 in diesem 3×3-Raster von Einheitsquadraten!

Also ein Quadrat der Seitenlänge √3. Welche sich als Kathete im rechtwinkligen Dreieck mit Hypotenuse 2 und andere Kathete 1 konstruieren lässt; Rolf wies darauf hin. Oder anders gesagt: √3 ist die Höhe im gleichseitigen Dreieck der Seitenlänge 2.

#Variante 1

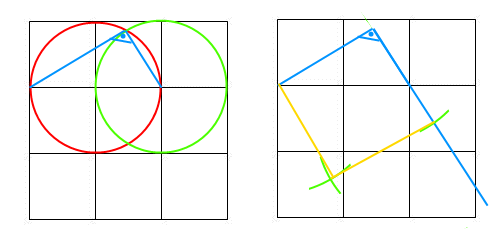
So hatten sich das wohl die meisten gedacht:

1. Kreisbogen um Y₁ mit Radius 2 schneidet x-Achse in P
2. Kreisbogen um X₁ mit Radius 2 schneidet y-Achse in R
   alternativ: Kreisbogen um O mit Radius OP schneidet y-Achse in R
3. Kreisbogen um P mit Radius OP (Stück oberhalb von P)
4. Kreisbogen um R mit demselben Radius OP (Stück rechts von R)
   Schnittpunkt mit (3) ist Q
   OPQR ist das gesuchte Quadrat.

Kosten: 12$ (wenn das Verbinden der Eckpunkte nicht Teil der Aufgabe ist)

#Variante 2

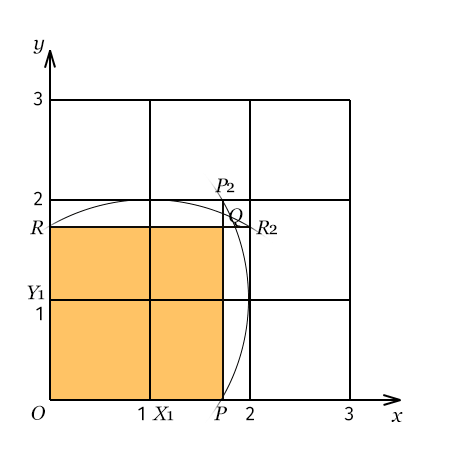
1. Kreisbogen um Y₁ mit Radius 2 schneidet x-Achse in P und Gerade y = 2 in P₂
2. Kreisbogen um X₁ mit Radius 2 schneidet y-Achse in R und Gerade x = 2 in R₂
3. Schnittpunkt der Geraden PP₂ und RR₂ ist Q
   OPQR ist das gesuchte Quadrat.

Kosten: ebenfalls 12$ (hier sind die Quadratseiten schon mit eingezeichnet)

#Variante 3

1. Kreisbogen um O mit Radius 2 schneidet Gerade y = 1 in P₁ und Gerade x = 1 in R₁
2. Kreisbogen um O mit Radius X₁R₁ schneidet x-Achse in P und y-Achse in R
3. Schnittpunkt der Geraden PP₁ und RR₁ ist Q
   OPQR ist das gesuchte Quadrat.

Kosten: 13$ (aber auch hier sind die Quadratseiten schon mit drin)

#Variante 4

@encoder hat noch einen ganz anderen Weg gefunden:

1. Konstruktion der √3 mit 2 Kreisen.
2. Abtragen der √3 auf dem Schenkel der kurzen Kathete.
3. 4. Eckpunkt des Quadrats wie in Variante 1

Kosten: 5 Kreise, 1 Linie (die andere Linie braucht man nicht), 18$. Teuer, aber originell.

#Variante 5

Der Grund, warum ich die von Felix in Spiel gebrachte Beziehung 1² + (√2)² = (√3)² einen „entscheidenden Gedanken“ nannte. √3 lässt sich auch konstruieren als Hypotenuse eines rechtwinkligen Dreiecks mit Katheten 1 und √2.

Oder ’ne Nummer kleiner: √³⁄₂ = ½√6 lässt sich konstruieren als Hypotenuse eines rechtwinkligen Dreiecks mit Katheten 1 und ½√2:

1. Zeichne die Diagonalen y = x und y = −x + 3, ihr Schnittpunkt ist M
2. Kreisbogen um A(1, 1) mit Radius AM schneidet Gerade y = 1 in B
3. C(1, 2). [Edit: C brauchen wir nicht] Kreisbogen um M mit Radius BC BX₁
   Schnittpunkte mit den Diagonalen sind die Eckpunkte des gesuchten Quadrats.

Kosten: 13$ (ohne Verbinden der Eckpunkte). Symmetrie hat halt ihren Preis.

LLAP 🖖