Mathematik zum Wochenende

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Am einfachsten geht’s wohl so:

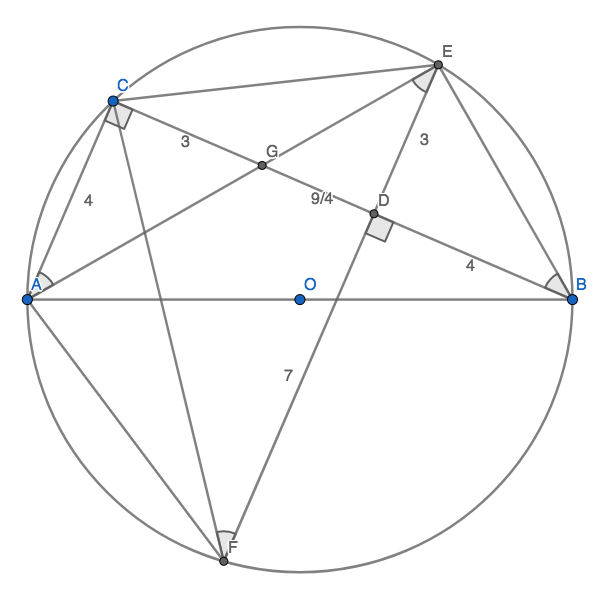
Winkel ACB ist nach Thales ein rechter; damit auch Winkel FDB (Stufenwinkel an geschnittenen Parallelen).

Die Winkel EAC, EFC, EBC und AEF sind gleich groß (Peripheriwinkel über CE bzw. Wechselwinkel an geschnittenen Parallelen).

Die Dreiecke AGC, EGD, BED und CFD stimmen in diesem Winkel und im rechten Winkel überein, sind also ähnlich. Ihre Kathetenlängen verhalten sich wie 3/4.

Wegen AC = BD ist DE = CG = 3.

GD = 3/4 × DE = 3/4 × 3 = 9/4;  CD = 3 + 9/4 = 21/4

FD = 4/3 × CD = 4/3 × 21/4 = 7;  FE = 7 + 3 = 10

Wegen AC ∥ FE ist das Sehnenviereck ACEF ein gleichschenkliges Trapez; die Dreiecke AFE und CFE sind kongruent. Ihre Fläche beträgt 1/2 × FE × CD = 1/2 × 10 × 21/4 = 105/4.

Bin ich da allein drauf gekommen? Natürlich nicht! 😡

Meine Lösung ging über Pythogoras und Heron und Wurzeln, die sich dann wegen (a + b)(a − b) = a² − b² wieder auflösten. Wenn ich mich dafür nicht so schämen würde nicht gerade unterwegs wäre, würde ich’s euch ja zeigen.

Ottogal war der Einfachheit da deutlich näher.

LLAP 🖖