Geometrie zur Wochenmitte

[Rolf B]

Hier ist meine Legepuzzle-Lösung. Eure Dreh-Lösung finde ich aber auch recht clever.

Ich teile das Umfeld des Innenquadrats geschickt auf und male die Teile aus:

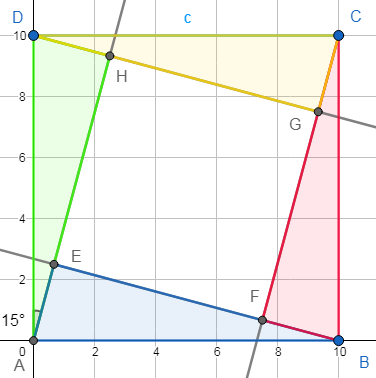
Die vier Dreiecke ABE, BCF, CDG und DAH sind kongruent (gleiche Seitenlängen, gleiche Winkel, etc). Zwei davon klappe ich auf die Rückseite und setze eine Raute zusammen (einen Rhombus, ein gleichseitiges Parallelogramm):

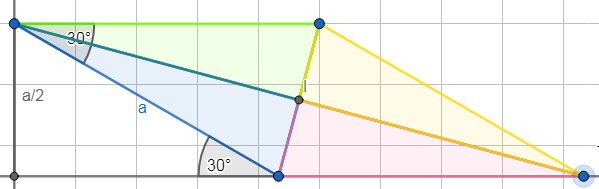
Da ich an den spitzen Ecken des Parallelogramms zwei 15° Winkel zusammengesetzt habe, beträgt der Winkel dort nun 30°. Die Kantenlänge aller Parallelogrammseiten, a, beträgt 10cm.

Der an der Basislinie eingezeichnete Winkel beträgt 30°. Begründbar als Wechselwinkel, Stufenwinkel oder Außenwinkel.

Von gleichschenkligen Dreiecken weiß ich, dass die Höhe zwischen zwei gleichen Schenkeln die Grundseite halbiert. D.h. wenn ich, wie links unten, ein rechtwinkliges Dreieck habe, in dem ein Winkel 30° beträgt, dann kann ich das nach unten spiegeln und erhalte ein gleichseitiges Dreieck mit Kantenlänge a, und die vertikal verlaufende Kante wird von der Basislinie halbiert (nicht eingezeichnet).

Ich habe also ein Parallelogramm, dessen Grundseite die Länge $$a$$ hat und dessen Höhe $$\frac{a}{2}$$ ist, die Fläche des vier Dreiecke und damit des Außenbereichs des Innenquadrats ist also $$\frac{1}{2}a^2$$. Dem Innenquadrat aus der Aufgabenstellung bleibt die andere Hälfte.

Rolf