Geometrie zur Wochenmitte – Lösung

[Rolf B]

Hallo ottogal,

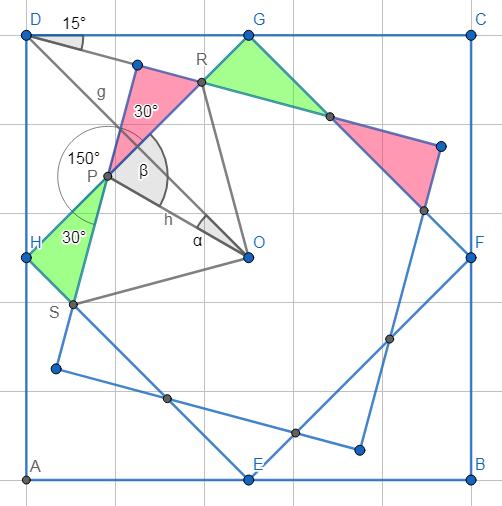
Wenn Du in diesem Bild beweisen kannst, dass α=15° ist, hast Du's geschafft.

Mathematisch formuliert:

Gegeben sind 2 Quadrate Q und Q' mit gleicher Größe und gleichem Mittelpunkt O. Eine Seite von Q sei a (im Bild unten CD), die an gleicher Stelle liegende Seite von Q' sei a'. g sei die Gerade, die durch O verläuft und senkrecht auf a steht.

Q' werde gegenüber Q um den Winkel ϕ (0° < ϕ < 90°) gedreht (im Fall unserer Aufgabe um 30°). Der Schnittpunkt von a und a' sei P, h sei die Gerade OP.

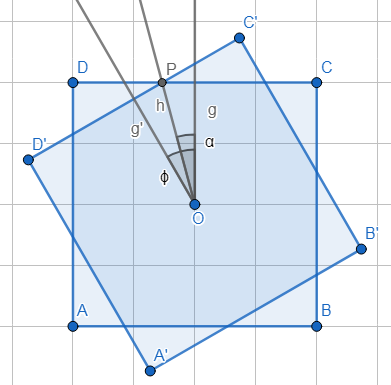
Behauptung: Der von den Geraden g und h eingeschlossene Winkel α ist halb so groß wie ϕ.

Erprobt man das mit Geogebra, ist die Behauptung richtig. Einen Beweis sehe ich gerade nicht. Vermutlich ist es total trivial...

Aber, wenn das der Fall ist, hat im ersten Bild β den Wert 75° und h ist Winkelhalbierende des 150° Winkels RPS, der dort die Spitze des Vierecks zwischen P und O bildet. Aus Symmetriegründen ist OR=OS, damit wäre dann ORPS ein Drachen und PR=PS. Und damit sind die roten und grünen Dreiecke nicht nur ähnlich, sondern auch kongruent.

Rolf