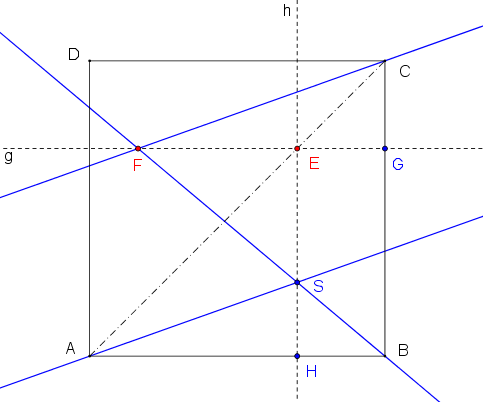
Ich löse mal auf:
O.B.d.A. legen wir ein Koordinatensystem so, dass $$A(0;0)$$, $$B(1;0)$$, $$C(1;1)$$ und $$D(0;1)$$ ist.
Die Lage von $$E$$ auf $$AC$$ wird durch einen Parameter $$a$$ bestimmt: $$E(a;a)$$.
Somit ist $$g=EG$$ mit $$G(1;a)$$ und $$h=EH$$ mit $$H(a;0)$$.
Für den Punkt $$F$$ auf $$g$$ brauchen wir einen weiteren Parameter $$b$$: $$F(b;a)$$.
Wir ermitteln die Gleichung der Geraden $$FB$$ in der Form $$y=mx+t$$.
Ihre Steigung ist
$$m=-\frac{GB}{FG}=-\frac{a}{1-b}$$.
Den Achsenabschnitt erhalten wir durch Einsetzen von $$F$$:
$$t=y-mx=a+\frac{a}{1-b} \cdot b=\frac{a}{1-b}$$.
Die Gleichung von $$FB$$ lautet also
$$y=-\frac{a}{1-b} \cdot x +\dfrac{a}{1-b}=\frac{a}{1-b} \cdot (1-x)$$.
Für den Schnittpunkt $$S$$ von $$FB$$ mit $$h$$ gilt $$x=a$$, somit
$$y=\frac{a}{1-b} \cdot (1-a) =\frac{a(1-a)}{1-b}$$.
Die Steigung der Geraden $$AS$$ ist daher
$$m_{AS}=\frac{SH}{AH}=\dfrac{\frac{a(1-a)}{1-b}}{a}=\frac{1-a}{1-b}$$.
Die Steigung der Geraden $$FC$$ hat aber den gleichen Wert:
$$m_{FC}=\frac{CG}{FG}=\frac{1-a}{1-b}$$.
Also sind die Geraden $$AS$$ und $$FC$$ parallel.