nicht angemeldet
Hallo in die Runde,
@Gunnar Bittersmann, @Rolf B und @Matthias Apsel haben mir Lösungen zukommen lassen, die ganz unterschiedliche Wege gehen, was sehr interessant ist. Deshalb schlage ich vor, dass ihr sie hier alle öffentlich macht.
Da meine eigene Lösung für die Quersumme 11 von eurer übereinstimmenden (69 Kombinationen) abwich, hatte ich sie erst noch zu korrigieren. 😟
(Mein "Widerspruch" an euch war voreilig und vorwitzig - so spiele ich auch Schach: Nach langem Abwägen mache ich den Zug, den ich aus guten Gründen zu allererst verworfen habe...).
Hier nun meine korrigierte Lösung:
Wir verwenden im Folgenden die Dreieckszahlen
$$D(1)=1$$, $$D(2)=3$$, $$D(3)=6$$, $$D(4)=10$$ ...
Die Dreieckszahl $$D(n)$$ zur Basis $$n$$ ist die Summe der natürlichen Zahlen von $$1$$ bis $$n$$ und errechnet sich nach Gauß zu $$D(n)=\frac{1}{2} n (n+1)$$.
Seien $$x$$, $$y$$, $$z$$ die drei Ziffern des Codes, $$s$$ ihre Summe.
(Ich schreibe hier $$s$$ statt $$q$$, weil ich beim Rechnen per Hand immer wieder $$q$$ mit $$9$$ verwechselt hatte.)
Somit gilt $$x+y=s-z$$ und $$0 \leq s \leq 27$$.
Wegen $$z \leq 9$$ gilt
|$$(1)\quad\quad x+y \geq s-9$$|
und wegen $$z \geq 0$$ gilt
|$$(2)\quad\quad x+y \leq s$$|
1. Fall: $$s \leq 9$$
Dann ist $$s-9 \leq 0$$. Wegen $$x \geq 0$$, $$y \geq 0$$ ist daher die Ungleichung (1) erfüllt.
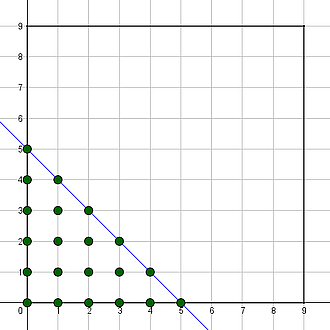
Die Punkte $$(x;y)$$, die die Ungleichung (2) erfüllen, liegen unterhalb oder auf der Geraden $$y=-x+s$$.
Sie bilden die Figur der Dreieckszahl $$D(s+1)$$, ihre Anzahl (also die Anzahl der Kombinationen mit diesen Bedingungen) ist also
$$k_1=D(s+1)=\frac{1}{2}(s+1)(s+2)$$.
Beispiel: $$s=5$$ ergibt $$k_1=D(6)=\frac{1}{2} \cdot 6 \cdot 7=21$$.
2. Fall: $$s \geq 18$$
Wir nutzen die Symmetrie der Situation aus: Es gibt genau so viele Kombinationen für die Summe $$s$$ wie für die Summe $$27-s$$.
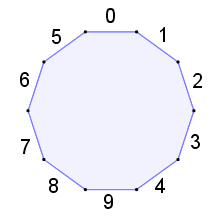
Begründung: Man stelle sich vor (o.B.d.A.), die Ziffern auf den Einstellrädern seien so angeordnet, dass je zwei gegenüberliegende sich zu 9 ergänzen:
Dann ist klar, dass es z.B. für die Summe $$s=20$$ genau gleich viele Kombinationen gibt wie für die Summe $$s=7$$; denn zur Kombination 794 mit $$s=20$$ gehört die komplementäre Kombination 205 mit $$s=7$$.
Für $$s \geq 18$$ berechnet man daher die Anzahl der Kombinationen mit $$t=27-s$$ gemäß Fall 1 zu $$k_2=D(t+1)=D(28-s)=\frac{1}{2}(28-s)(29-s)$$.
Beispiel: $$s=20$$ ergibt $$k_2=D(28-20)=D(8)=\frac{1}{2} \cdot 8 \cdot 9=36$$.
3. Fall: $$9 < s < 18$$
Also ist hier $$0 < s-9 < 9$$.
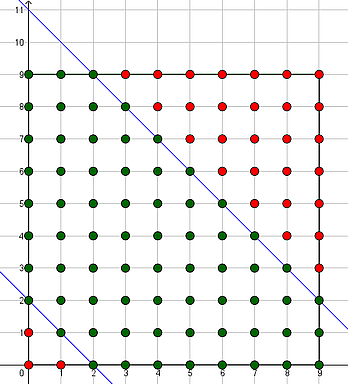
Die Punkte, die die Ungleichungen (1) und (2) erfüllen, liegen zwischen oder auf den parallelen Geraden
$$g_1$$: $$y=-x+(s-9)$$ und
$$g_2$$: $$y=-x+s$$
Diejenigen von den 100 Punkten der möglichen (x;y)-Paare, die nicht beide Ungleichungen erfüllen, verteilen sich auf zwei Dreieckszahl-Figuren:
Die untere hat wegen $$g_1(0)=s-9$$ die Basis $$s-9$$ und enthält somit
$$D(s-9)=\frac{1}{2}(s-9)(s-8)$$ Punkte;
die obere hat wegen $$g_2(9)=s-9$$ die Basis $$9-(s-9)=18-s$$ und enthält somit
$$D(18-s)=\frac{1}{2}(18-s)(19-s)$$ Punkte.
Beides zusammen ergibt
$$D(s-9)+D(18-s)=\tfrac{1}{2} \left( (s-9)(s-8)+(18-s)(19-s) \right)=$$
$$=\tfrac{1}{2} \left( s^2-17s+72+342-37s+s^2 \right)=$$
$$= s^2-27s+207=$$
$$=207-s(27-s)$$
Dies ist die Anzahl der Kombinationen, die die Bedingung nicht erfüllen. Die Anzahl der gesuchten Kombinationen ist daher
$$k_3=100-(207-s(27-s))=s(27-s)-107$$.
Beispiel: $$s=11$$ ergibt $$k_3=11 \cdot 16 -107=69$$.
Diese Aufgabe habe ich mir übrigens beim Warten am Flughafen ausgedacht.
Praktische Erfahrung war vorhanden: Vor Jahren habe ich mal ein Kofferschloss (ohne Kenntnis der Quersumme) mit mehr als 800 Versuchen geknackt... 😉 (Feyman hätte es sicher schneller geschafft.)
Beste Grüße
ottogal
Matthias Apsel
JürgenB
Gunnar Bittersmann
Rolf B