Mathematik für unterwegs - Lösung
bearbeitet vonHallo ottogal,
deine Lösung ist mir zum schnellen Überfliegen zu hoch, ich verstehe kein Wort.
Matthias Lösung ist clever.
Meine Lösung war brute force: Ich habe mir erstmal für alle Kombinationen aus 2 Ziffern die Quersummen aufgeschrieben. Dabei habe ich nur die geordneten Paare (x,y) mit x<=y betrachtet, weil ich nachher sowieso Permutationen bilde und keine Duplikate haben will. Es gibt pro Quersumme ein (q=0,18) bis fünf (q=8,9,10) geordneter Zahlenpaare mit dieser Quersumme, insgesamt 1+1+2+2+3+3+4+4+5+5+5+4+4+3+3+2+2+1+1=59 Zahlenpaare. Für jedes dieser Paare habe ich eine 3-er Gruppe von Spalten in Excel aufgemacht, sowie Zeilen für die Quersummen 0-27. Dann habe ich jedes Paar mit den Ziffern 0-9 kombiniert und die Kombination in der Zeile mit der entsprechenden Quersumme eingetragen. Auch hier habe ich darauf geachtet, geordnete Tripel zu erhalten, d.h. wenn die Einzelziffer größer war als die erste Stelle des Paares, habe ich die Kombination nicht gezählt.
Ein solches Tripel zählt nun für 1, 3 oder 6 mögliche Kombinationen, je nach dem, ob es aus 1, 2 oder 3 unterschiedlichen Ziffern besteht. Mit etwas Excel-Akrobatik kann man das pro Kombination bestimmen.
D.h. ich habe nun eine Gruppe aus 3 Spalten und 2 Zeilen, die so aussieht:
~~~
z xy _
_ _ k
~~~
z und xy sind Einzelziffer und Zahlenpaar, k die Anzahl der Kombinationen, die sich daraus bilden lassen. k steht eine Zeile tiefer um leichter Summieren zu können. Mit etwas bedingter Formatierung habe ich die zu zählenden Kombinationen noch hervorgehoben, das sieht dann so aus:
[](/images/2a955da0-88a2-4bb6-ba69-d25179b8c314.png)
Betrachtet man nur die Quersummen und die auszuprobierenden Kombis für diese Quersumme, gibt's eine schöne Glocke:
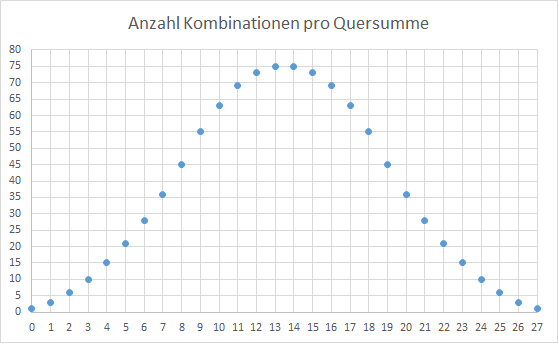
Zu doof für Mathe, aber ein Wizard mit Excel 😂
_Rolf_
--
sumpsi - posui - clusi


