Mathematik zum Wochenende - Lösung

[Matthias Apsel]

Hallo Matthias Apsel,

In maximal wieviele Gebiete kann die Ebene durch n Geraden geteilt werden?

Ob die Argumentationskette wirklich als Beweis gilt, …

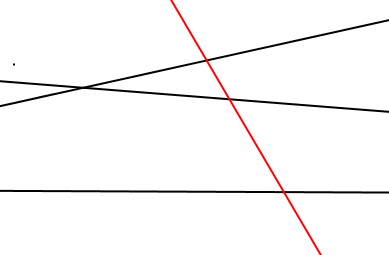
Wenn eine Gerade eine schon irgendwie durch n Geraden unterteilte Ebene so teilen soll, dass möglichst viele neue Gebiete entstehen soll, muss diese Gerade alle vorhandenen Geraden so schneiden, dass keine Schnittpunkte zusammenfallen. Dass sie keine der vorhandenen Geraden mehr als einmal schneiden kann, sollte auch klar sein.

Deshalb verläuft die neue Gerade durch n + 1 Gebiete, das zwischen „Anfang der Ebene“ und erster Gerade, das zwischen erster und zweiter Gerade, … das zwischen vorletzter und letzter Gerade und das zwischen letzter Gerade und dem „Ende der Ebene“.

Die Zählung erfolgt dabei aus der Sicht der neuen Geraden und ist nicht etwa die Reihenfolge der Erzeugung der Vorgängergeraden.

Die n-te Gerade kann also maximal n + 1 neue Gebiete erzeugen. Es gilt

$$g = \sum_{k=1}^n i + 1 = 1 + \sum_{k=1}^n i = 1 + \frac{n}{2} \cdot (n + 1) = \frac{n^2 + n + 2}{2}$$

Wer das nun beweisen möchte, kann das gern mit vollständiger Induktion tun.

Richtige Antworten kamen von @encoder und @Rolf B. Auch das, was @Julia schrieb war (auf den flüchtigen Blick) richtig.

Eine kleine Zusatzaufgabe: Wieviele Schnittpunkte zwischen n Geraden kann es maximal geben?

Bis demnächst
Matthias