Informatik zum Jahresanfang

[Gunnar Bittersmann]

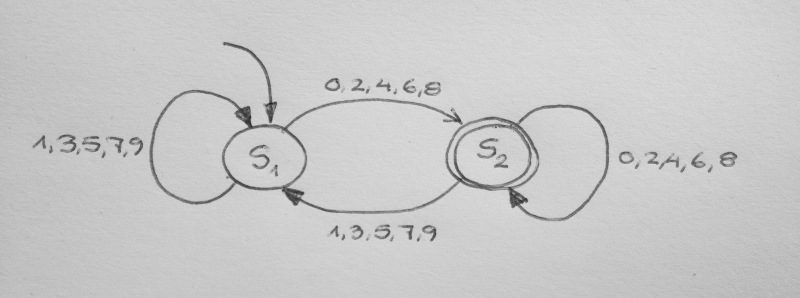
Das Bild zeigt einen endlichen Automaten, der sich bei der Eingabe einer Ziffernfolge nur dann im Endzustand (dargestellt durch doppelte Linie) befindet, wenn die dadurch eingegebene Zahl durch 2 teilbar ist. (Führende Nullen sollen erlaubt sein.)

1. Formal beschrieben ist dieser durch ein Quintupel (S, s₁, Σ, δ, F) mit:
   S – Menge der Zustände, in dem Fall S = {s₁, s₂}
   s₁ ∈ S – Startzustand
   Σ – Menge der Eingabesymbole (Eingabealphabet), in dem Fall Σ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
   δ: S × Σ → S – Zustandsübergangsfunktion, in dem Fall $$\delta(s_i, \sigma) = \begin{cases} s_2, & \text{wenn }\sigma ∈ {0, 2, 4, 6, 8}
   s_1, & \text{wenn }\sigma ∈ {1, 3, 5, 7, 9} \end{cases}; i ∈ {1, 2}$$
   F ⊆ S – Menge der Endzustände, in dem Fall F = {s₂}

Die Aufgabe ist, einen endlichen Automaten zu bauen, der sich nur dann in einem Endzustand befindet, wenn die eingegebene Zahl durch 4 teilbar ist. Grafische Darstellung genügt. (Wie oben: führende Nullen sind erlaubt.)

LLAP 🖖