Informatik zum Jahresanfang
bearbeitet von@@Gunnar Bittersmann
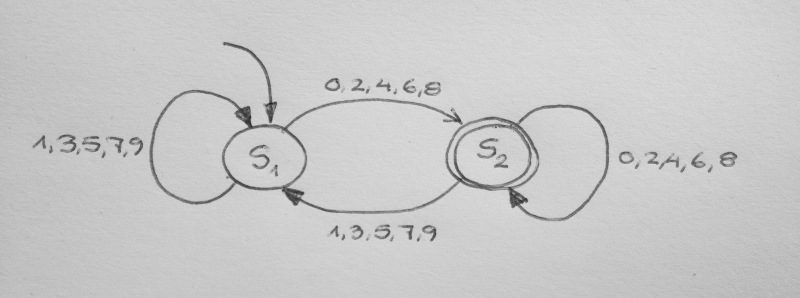
> Das Bild zeigt einen endlichen Automaten, der sich bei der Eingabe einer Ziffernfolge nur dann im Endzustand (dargestellt durch doppelte Linie) befindet, wenn die dadurch eingegebene Zahl durch 2 teilbar ist. (Führende Nullen sollen erlaubt sein.)
>
> [](/images/e1c2c44c-9fbb-44ea-bffc-c2a26744ba2b.jpeg)
Erklärung, wie das zu verstehen ist; am Beispiel von 9876:
Der Automat ist anfangs im Zustand *S*₁; das ist kein Endzustand.
Durch Eingabe einer 9 bleibt der Automat im Zustand *S*₁. Kein Endzustand; 9 ist nicht durch 2 teilbar.
Durch Eingabe einer 8 geht der Automat in den Zustand *S*₂. Das ist ein Endzustand; 98 ist durch 2 teilbar.
Durch Eingabe einer 7 geht der Automat wieder in den Zustand *S*₁. (Das kann er tun. Endzustand heißt, dass der Automat am Ende in dem Zustand sein kann; nicht aber, das er den Zustand nicht wieder verlassen kann, wenn er sich zwischendurch darin befindet.) *S*₁ ist kein Endzustand; 987 nicht durch 2 teilbar.
Durch Eingabe einer 6 geht der Automat wieder in den Zustand *S*₂. Endzustand; 9876 ist durch 2 teilbar.
LLAP 🖖
--
*„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“* —Kurt Weidemann


