Informatik zum Jahresanfang – noch mehr Teiler
bearbeitet von@@Gunnar Bittersmann
> Das Bild zeigt einen endlichen Automaten, der sich bei der Eingabe einer Ziffernfolge nur dann im Endzustand (dargestellt durch doppelte Linie) befindet, wenn die dadurch eingegebene Zahl durch 2 teilbar ist. (Führende Nullen sollen erlaubt sein.)
>
> [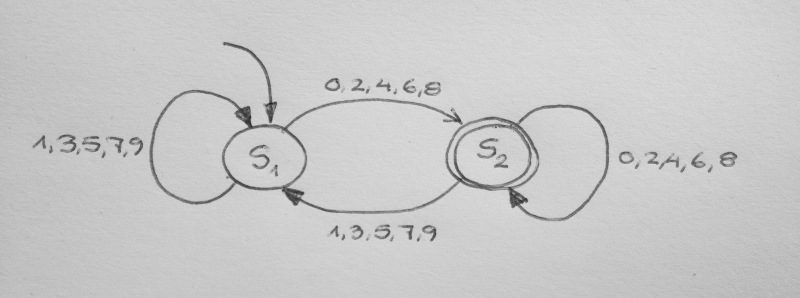](/images/e1c2c44c-9fbb-44ea-bffc-c2a26744ba2b.jpeg)
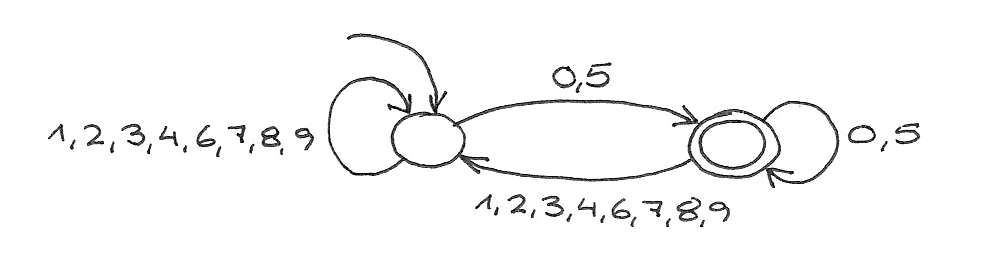
Durch geringfügige Modifikation wird daraus ein Automat, der durch 5 teilbare Zahlen erkennt:
{:width="600"}
Und einer, der durch 10 teilbare Zahlen erkennt:
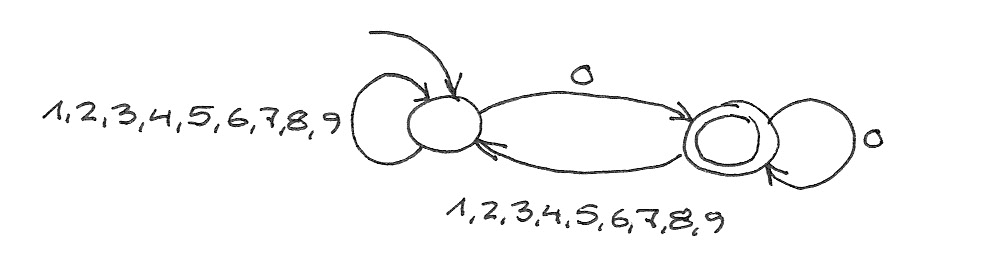{:width="600"}
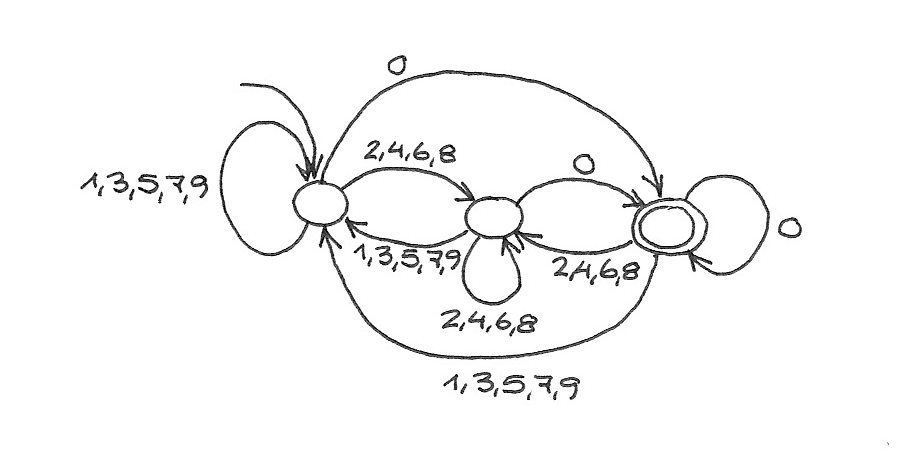
Und wenn man einen 2er und einen 10er hinternander setzt, erhält man einen Automaten, der durch 20 teilbare Zahlen erkennt. Hier in der delfixschen Gesichtsform:
{:width="600"}
So, was haben wir denn jetzt? Teilbarkeit durch 2, 4, 5, … Moment, was ist mit der 3?
Hier die Aufgabe für alle, die mit der 8 fertig sind oder mit der 8 *fertig* sind: 😉
Baue einen endlichen Automaten, der sich nur dann in einem Endzustand befindet, wenn die eingegebene Zahl durch 3 teilbar ist.
Und wenn man den hat, hat man auch durch geringfügige Modifikation den für 6. Und den für 15.
LLAP 🖖
--
*„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“* —Kurt Weidemann


