Informatik zum Jahresanfang – Auflösung der Zusatzaufgabe für 8
bearbeitet von@@Gunnar Bittersmann
> > … wenn die dadurch eingegebene Zahl durch 2 teilbar ist.
> > … wenn die eingegebene Zahl durch 4 teilbar ist.
>
> Was kann denn jetzt wohl kommen?
>
> Die Zusatzaufgabe ist, eine endlichen Automaten zu bauen, der sich nur dann in einem Endzustand befindet, wenn die eingegebene Zahl durch 8 teilbar ist.
Bei Teilbarkeit durch 2 muss man sich die letzte Stelle ansehen, bei Teilbarkeit durch 4 die letzten beiden, bei Teilbarkeit durch 8 die letzten drei.
Ein regulärer Ausdruck, der durch 8 teilbare Zahlen erkennt:
[048]?[08]\|[26]4\|[159]6\|[37]2 \| [0-9]\*(\[02468]([048][08]\|[26]4\|[159]6\|[37]2) \| \[13579]([048]4\|[26][08]\|[159]2\|[37]6))
(Ich hab zur besseren Übersichtlichkeit Leerzeichen gesetzt. Die sind natürlich hier keine Symbole.)
Endlicher Automat: ein [Pentakel](https://de.wikipedia.org/wiki/Pentagramm#Pentakel).
[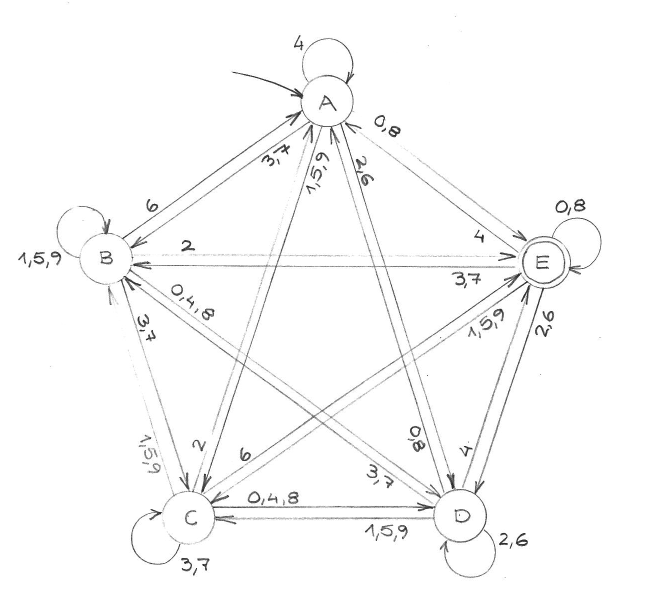](/images/d05edabd-754a-4b86-b660-b5b9ab050c48.png)
Darstellung analog zur dedlfixschen Gesichtsform beim 4er: ein keltisches Ornament?
[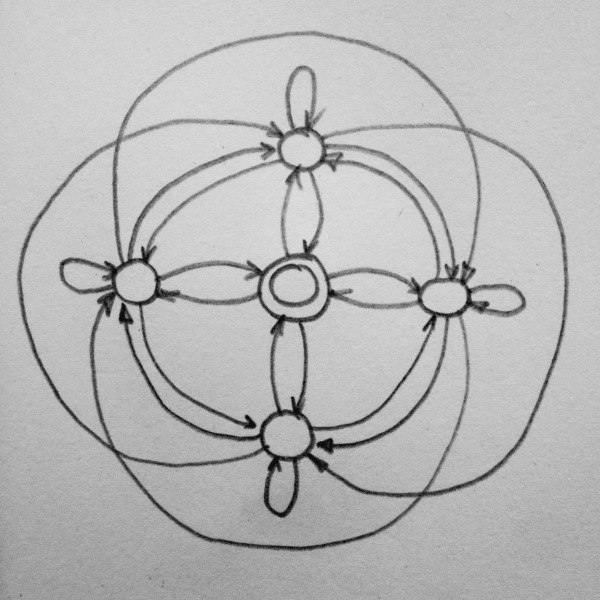](/images/773f6cbb-5c25-4aeb-9d3a-06735c4706a3.jpeg)
(Fehlende Beschriftung gewollt, aber ich hab mal wieder keinen Startpfeil gemalt und der Übergang vom Endzustand zu sich selbst fehlt. Aber das würde nur die Symmetrie stören. 😉)
LLAP 🖖
--
*„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“* —Kurt Weidemann
Informatik zum Jahresanfang – Auflösung der Zusatzaufgabe für 8
bearbeitet von@@Gunnar Bittersmann
> > … wenn die dadurch eingegebene Zahl durch 2 teilbar ist.
> > … wenn die eingegebene Zahl durch 4 teilbar ist.
>
> Was kann denn jetzt wohl kommen?
>
> Die Zusatzaufgabe ist, eine endlichen Automaten zu bauen, der sich nur dann in einem Endzustand befindet, wenn die eingegebene Zahl durch 8 teilbar ist.
Bei Teilbarkeit durch 2 muss man sich die letzte Stelle ansehen, bei Teilbarkeit durch 4 die letzten beiden, bei Teilbarkeit durch 8 die letzten drei.
Ein regulärer Ausdruck, der durch 8 teilbare Zahlen erkennt:
[048]?[08]\|[26]4\|[159]6\|[37]2\|[0-9]\*(\[02468]([048][08]\|[26]4\|[159]6\|[37]2)\|\[13579]([048]4\|[26][08]\|[159]2\|[37]6))
Endlicher Automat: ein [Pentakel](https://de.wikipedia.org/wiki/Pentagramm#Pentakel).
[](/images/d05edabd-754a-4b86-b660-b5b9ab050c48.png)
Darstellung analog zur dedlfixschen Gesichtsform beim 4er: ein keltisches Ornament?
[](/images/773f6cbb-5c25-4aeb-9d3a-06735c4706a3.jpeg)
(Fehlende Beschriftung gewollt, aber ich hab mal wieder keinen Startpfeil gemalt und der Übergang vom Endzustand zu sich selbst fehlt. Aber das würde nur die Symmetrie stören. 😉)
LLAP 🖖
--
*„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“* —Kurt Weidemann


