Informatik zum Jahresanfang – noch eine Variation
bearbeitet von@@Matthias Apsel
> > Hier sieht man auch schön, wann sich ein Automat nicht reduzieren lässt:
>
> Der Automat könnte sich aber trotzdem reduzieren lassen. Schließlich hat er noch andere Zustände.
Ja, die wären auch jeweils paarweise zu prüfen.
Und wo ich das schon in einer DM erläutert hatte, stelle ich’s auch hier rein.
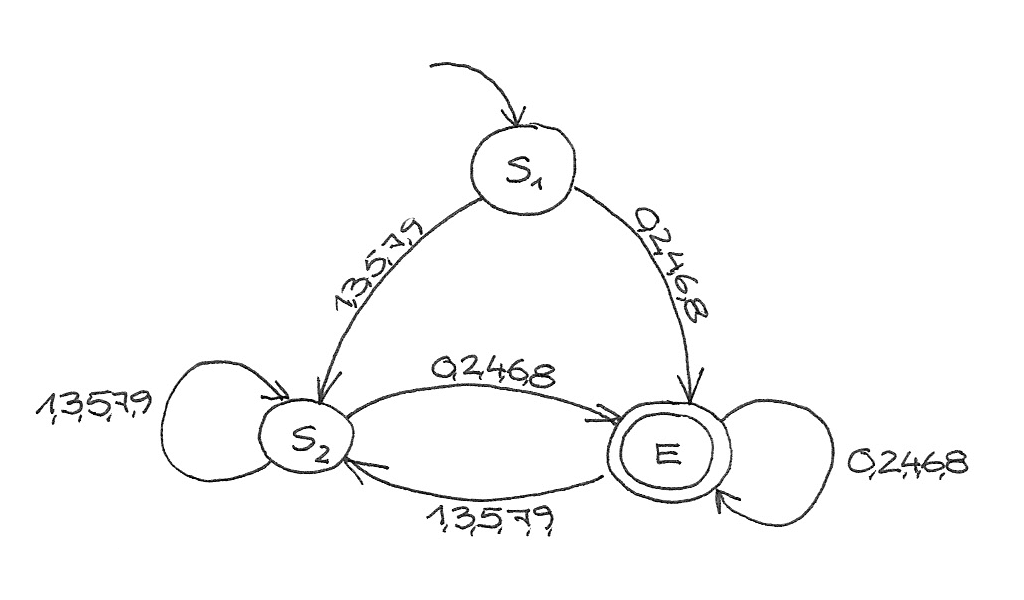
Schauen wir uns diesen 2er Automaten an:
{:width="512"}
Von *S*₁ gelangt man mit 1, 3, 5, 7, 9 zu *S*₂ und mit 0, 2, 4, 6, 8 zu *E*.
Von *S*₂ gelangt man mit 1, 3, 5, 7, 9 zu *S*₂ und mit 0, 2, 4, 6, 8 zu *E*.
Beides sind keine Endzustände, deshalb kann man *S*₁ und *S*₂ zusammenfassen:
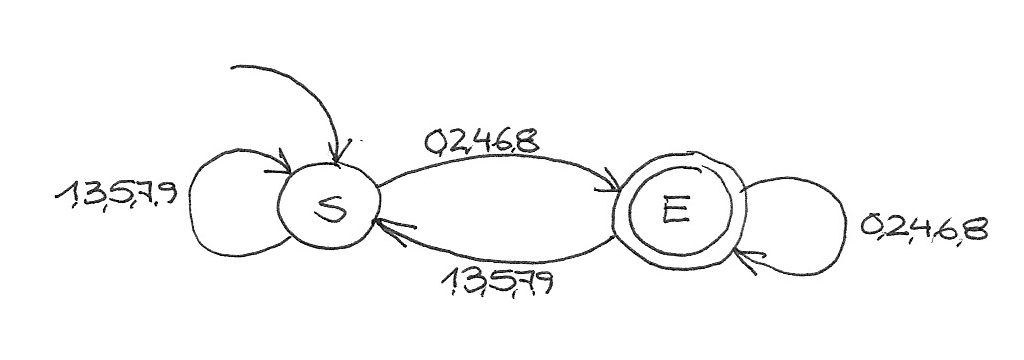{:width="512"}
Das o.g. Kriterium allein reicht aber nicht.
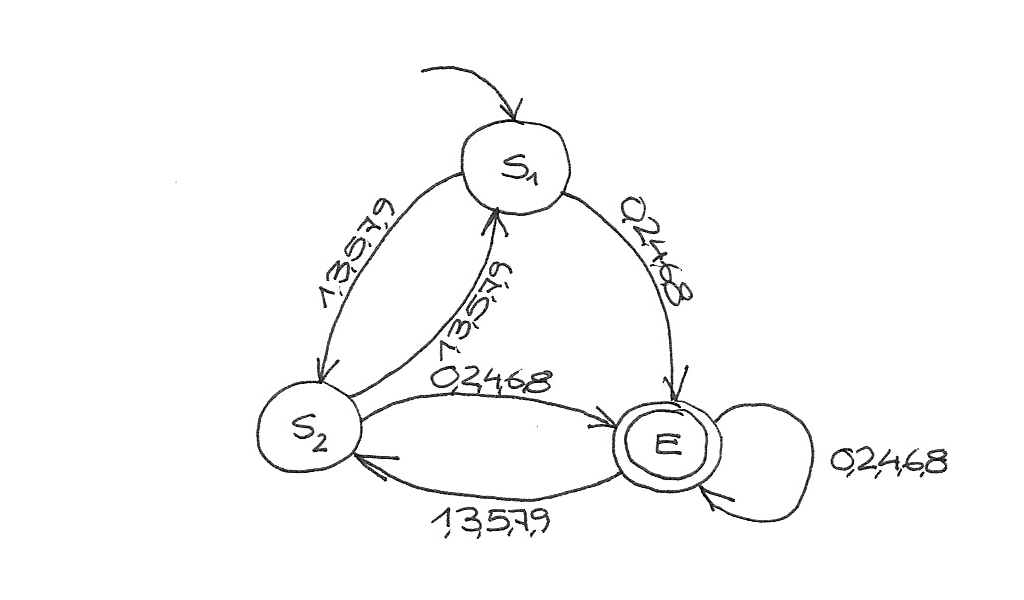{:width="512"}
Von *S*₁ gelangt man mit 1, 3, 5, 7, 9 zu ***S*₂** und mit 0, 2, 4, 6, 8 zu *E*.
Von *S*₂ gelangt man mit 1, 3, 5, 7, 9 zu ***S*₁** und mit 0, 2, 4, 6, 8 zu *E*.
Trotzdem kann man auch diesen Automaten genauso reduzieren.
Da müsste ich nochmal drüber nachdenken oder nachlesen (vielleicht hab ich sogar noch meine Unterlagen aus Theoretischer Informatik von der Uni irgendwo im Schrank), wie man das auch noch mit reinbekommt.
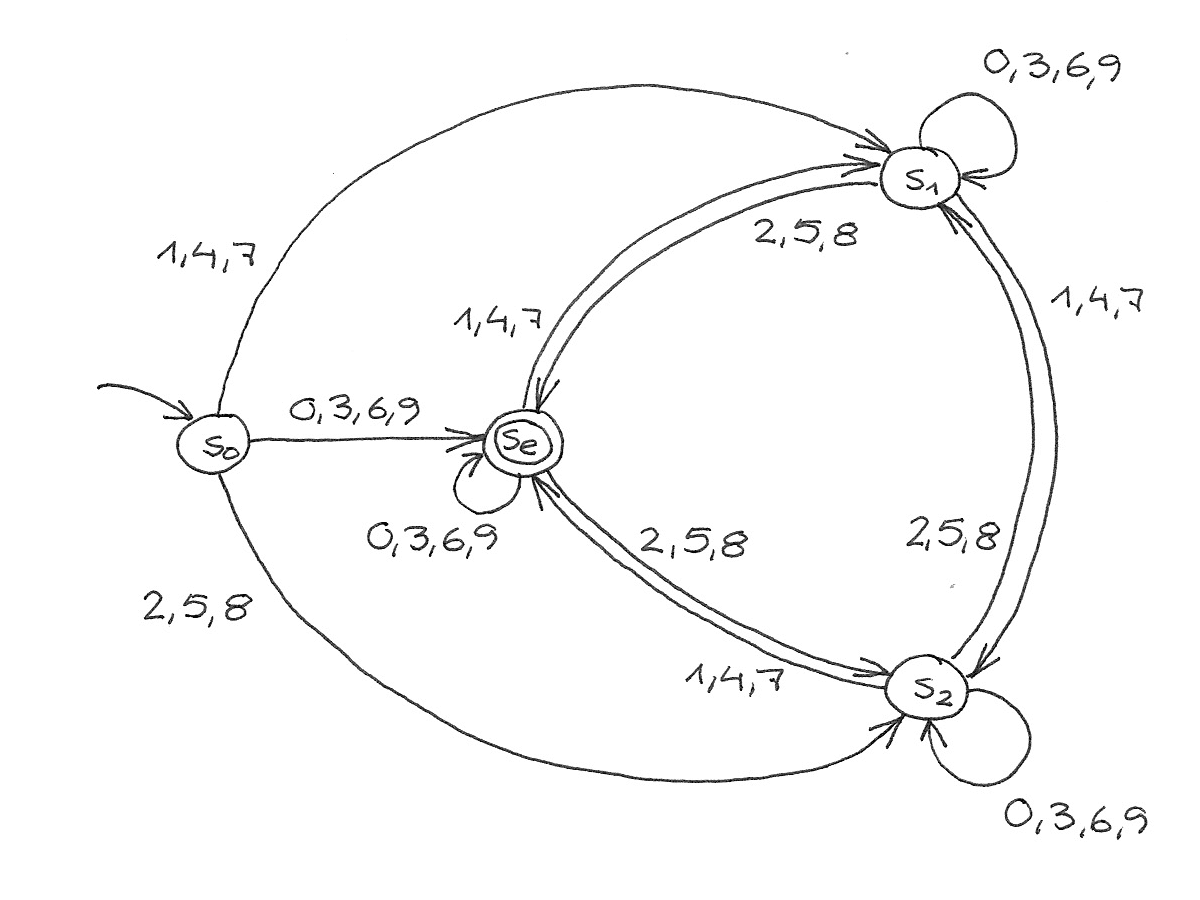
Schauen wir und nochmal den 3er Automaten an:
{:width="600"}
Von *s*₀ mit 1, 4, 7 zu *s*₁, mit 2, 5, 8 zu *s*₂ und mit 0, 3, 6, 9 zu *s*ₑ.
Von *s*ₑ mit 1, 4, 7 zu *s*₁, mit 2, 5, 8 zu *s*₂ und mit 0, 3, 6, 9 zu *s*ₑ.
Stimmt auch überein. Wenn man nun *s*₀ und *s*ₑ zusammenfassen würde:
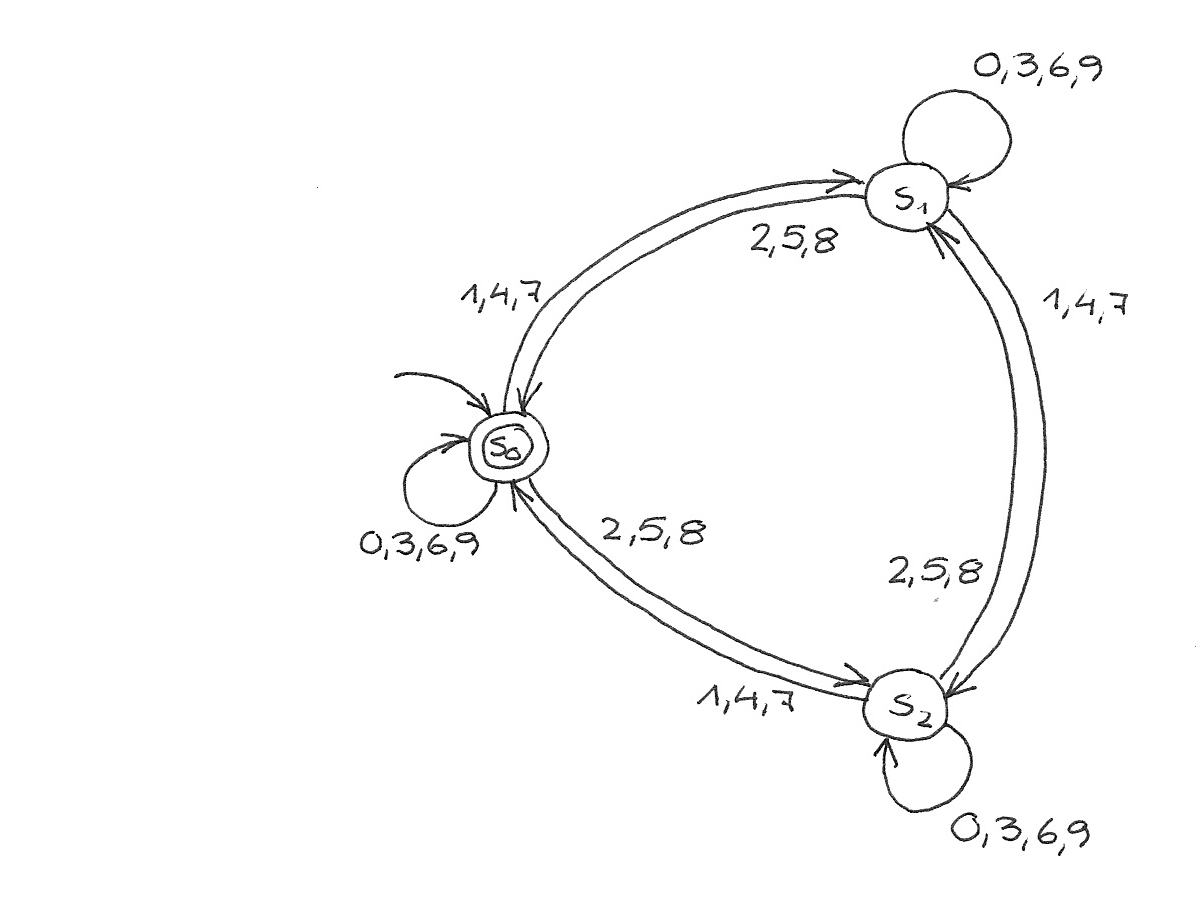{:width="600"}
Das hatten wir doch schon! 😉
*s*₀ und *s*ₑ darf man nicht zusammenfassen, da der eine ein Endzustand ist, der andere aber nicht.
LLAP 🖖
--
*„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“* —Kurt Weidemann


