Hallo Matthias Apsel,
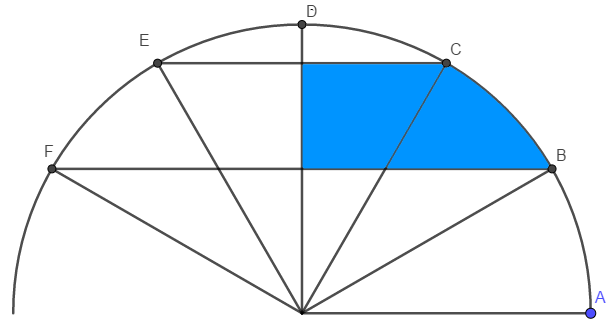
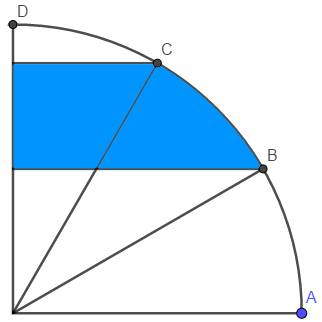
die blaue Fläche ist die halbe Differenz der Kreissegmente mit den Zentriwinkeln $$\frac{2}{3}\pi$$ und $$\frac{\pi}{3}$$.
$$\mathrm{A} = \frac{1}{2} \frac{r^2}{2} \left( \left( \frac{2}{3}\pi - sin\frac{2}{3}\pi \right) - \left( \frac{\pi}{3} - sin\frac{\pi}{3} \right)\right) = \frac{\pi}{12}r^2$$
Diesen Lösungsweg beschritten @Rolf B, @Gunnar Bittersmann, @MudGuard (leider fehlerhaft, mit demselben Fehler, den auch ich zuerst gemacht habe).
Auf Twitter fand ich die Lösung „Trapez + Segment“, …
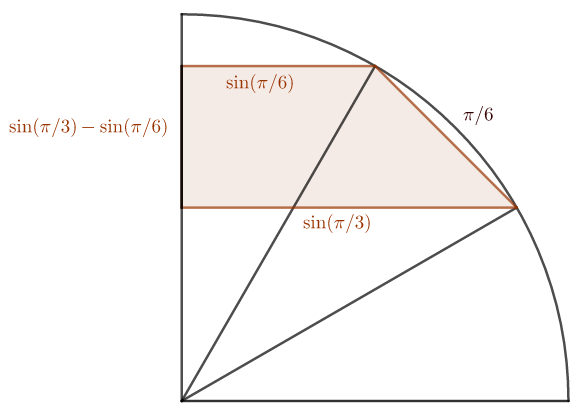
$$\mathrm{A}=\frac{r^2}{2}\left(sin\frac{\pi}{3}-sin\frac{\pi}{6}\right)\left(sin\frac{\pi}{3}+sin\frac{\pi}{6}\right) + \frac{\pi}{12}r^2-\frac{1}{2}sin\frac{\pi}{6}$$
$$\mathrm{A}=\frac{r^2}{2}\left(sin^2\frac{\pi}{3}-sin^2\frac{\pi}{6}\right) + \frac{\pi}{12}r^2-\frac{r^2}{2}sin\frac{\pi}{6}$$
$$\mathrm{A}=\frac{r^2}{2}\left(\frac{3}{4}-\frac{1}{4}\right) + \frac{\pi}{12}r^2-\frac{r^2}{4}$$
… die mich auf die Idee brachte nach dem Umfang zu fragen.
@Gunnar Bittersmann hat die Integralrechnung verwendet: $$\mathrm{A}=\int\limits_{sin\frac{\pi}{6}}^{sin\frac{\pi}{3}} \sqrt{1-x^2} \mathrm{d}x$$
Aber die in meinen Augen geschickteste Beweisidee kam von (ich bin fast geneigt zu sagen wie immer) von @ottogal. Die dampfe ich mal auf ein Minimum zusammen um sie nicht gleich in Gänze zu verraten, sondern im Gegenteil zum Nachdenken anzuregen:
Durch die Drittelung des Bogens entstehen Kreissektoren der Fläche $$\frac{\pi}{12}r^2$$. Wie man sehen kann, ist eine Fläche, so groß wie zwei dieser Sektoren, nicht gefärbt. Chapeau.
Bis demnächst
Matthias
Du kannst das Projekt SELFHTML unterstützen,
indem du bei Amazon-Einkäufen Amazon smile (Was ist das?) nutzt.