nicht angemeldet
Hallo in die kleine Runde,
hier meine Lösung:
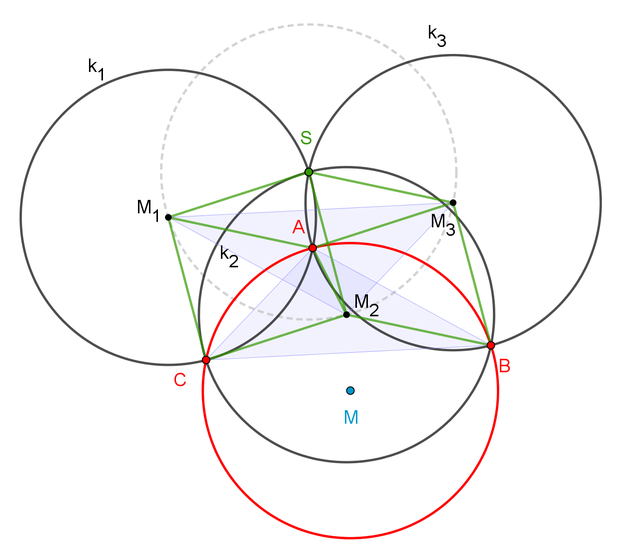
Die grün eingetragenen Strecken sind Radien der gegebenen Kreise, haben also alle die gleiche Länge $$r$$.
Die Vierecke $$SM_1CM_2$$, $$SM_1AM_3$$ und $$SM_2BM_3$$ sind daher Rauten.
Insbesondere gilt daher:
$$CM_1||BM_3$$ und $$|CM_1|=|BM_3|\quad$$ (1).
Nun gilt der Hilfssatz:
Ein Viereck mit zwei parallelen, gleichlangen Seiten ist ein Parallelogramm; d.h. auch seine andern beiden Seiten müssen parallel und gleich lang sein.
(Denn eine Diagonale des Vierecks zerlegt dieses in zwei nach dem SWS-Satz kongruente Dreiecke.)
Mit dem Hilfssatz folgt aus (1):
Das Viereck $$CBM_3M_1$$ ist ein Parallelogramm, und daher ist
$$|BC|=|M_1M_3|$$.
Ganz entsprechend zeigt man:
Das Viereck $$CM_2M_3A$$ ist ein Parallelogramm, und daher ist
$$|CA|=|M_3M_2|$$.
Das Viereck $$M_2BAM_1$$ ist ein Parallelogramm, und daher ist
$$|BA|=|M_1M_2|$$.
Somit stimmen die Dreiecke $$\triangle ABC$$ und $$\triangle M_2M_1M_3$$ in allen drei Seiten überein und sind daher kongruent. Ihre Umkreise (der rote und der gestrichelte) haben deshalb den gleichen Radius.
q.e.d.
Nur Gunnar hat eine Lösung mitgeteilt, mit einer anderen Herleitung der Kongruenz der beiden Dreiecke.
@Gunnar Bittersmann : Magst du sie hier zeigen?
Viele Grüße
ottogal
Gunnar Bittersmann
Rolf B