nicht angemeldet
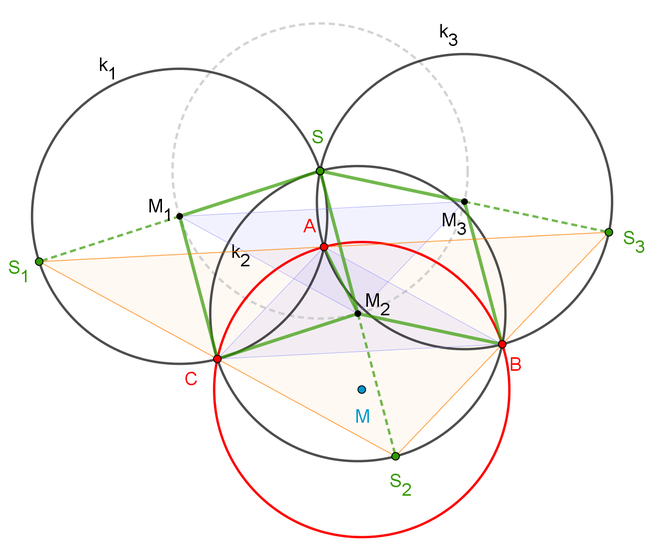
Ich habe noch einen anderen Beweis für die Kongruenz der Dreiecke $$\triangle M_1M_2M_3$$ und $$\triangle BAC$$ gefunden:
Wendet man auf das Dreieck $$\triangle M_1M_2M_3$$ eine zentrische Streckung mit Zentrum $$S$$ und Faktor $$2$$ an, so erhält man das Dreieck $$\triangle S_1S_2S_3$$; dabei kommen $$S_1$$, $$S_2$$, $$S_3$$ auf den Kreisen $$k_1$$, $$k_2$$, $$k_3$$ zu liegen (weil die Radien zu Durchmessern getreckt werden). Infolge der Strahlensätze geht $$S_1S_2$$ durch $$C$$ und $$S_2S_3$$ durch $$B$$.
Somit gilt: Die Dreiecke $$\triangle M_1M_2M_3$$ und $$\triangle S_1S_2S_3$$ sind ähnlich, der Ähnlichkeitsfaktor ist $$\frac{1}{2}$$.
Andererseits ist $$\triangle BAC$$ das Mittendreieck von $$\triangle S_1S_2S_3$$ und daher ebenfalls ähnlich zu diesem, und der Ähnlichkeitsfaktor ist auch $$\frac{1}{2}$$.
Daraus folgt die Kongrenz der Dreiecke $$\triangle M_1M_2M_3$$ und $$\triangle BAC$$.
Gunnar Bittersmann
Rolf B