Mathematik zur Abkühlung – Lösung
bearbeitet vonHallo Matthias Apsel,
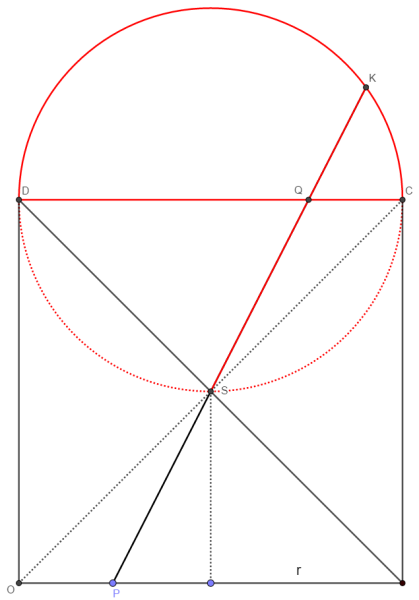
wie so oft, ist die Wahl der richtigen Hilfslinie wichtig. Diesmal ist es die andere Hälfte des Kreises.
[](/images/59dee06a-e3d4-11ea-a122-b42e9947ef30.png)
Um Brüche zu vermeiden, nehmen wir nicht die Seitenlänge des Quadrates, sondern den Radius des Kreises als Parameter. Die Länge der Strecke OP sei _p_.
DC und SK sind Sehnen desselben Kreises. Für die gilt der Sehnensatz, den @ottogal auch verwendet hat, allerdings ohne ihn zu nennen, dafür fällt bei ihm der Beweis quasi nebenbei mit ab.
Sehnensatz: Das Produkt der Sehnenabschnitte der einen Sehne ist gleich dem Produkt der Sehnenabschnitte der anderen Sehne.
Damit gilt:
DQ = 2*r* - _p_
QC = _p_
SQ = PS
PS lässt sich über den Pythagoras ermitteln: $$\overline{PS}^2=r^2+(r-p)^2$$, für QK kann der Sehnensatz verwendet werden.
$$QK = \frac{(2r-p) \cdot p}{\sqrt{r^2 + (r-p)^2}}$$
Damit ist Teil b) erledigt.
Für Teil a) können wir noch ein bisschen addieren und erhalten:
$$SK = \frac{2r}{\sqrt{r^2 + (r-p)^2}}$$
Mit _r_ = 12 und _p_ = 3 ergibt sich SK = 96/5.
Alternativ kann man auch hier den Sehnensatz verwenden. Das Dreieck zur Berechnung von PS hat die Katheten 9 und 12, also ist PS = SQ = 15 (3-4-5-Dreieck). Die beiden anderen Sehnenabschnitte sind 3 und 21.
Damit ist die gesuchte Streckenlänge $$15 + \frac{3 \cdot 21}{15}$$
Bis demnächst
Matthias
--
Du kannst das Projekt SELFHTML unterstützen,
indem du bei Amazon-Einkäufen [Amazon smile](https://smile.amazon.de/ch/314-570-45498) ([Was ist das?](https://www.amazon.de/gp/help/customer/display.html?ie=UTF8&nodeId=202035970])) nutzt.


