Mathematik zum Schokoladenstreit – Lösung

[Gunnar Bittersmann]

@@Gunnar Bittersmann

(Für dies „key insight“ muss man aber nicht die Vektorrechnung bemühen; das lässt sich auch geometrisch zeigen. @Tabellenkalk⁠s Herleitung begann mit „Wie man leicht sieht“ – da schrillten bei mir erstmal die Alarmglocken. 🤯 Man kann’s aber wirklich sehen.)

@ottogal hat’s dann auch in Worte gefasst:

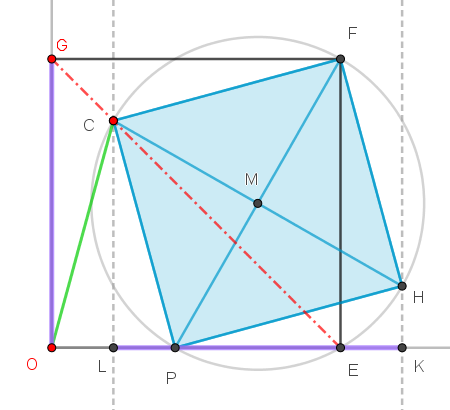
Wir betrachten die Beziehung zwischen dem großen Quadrat OEFG und dem blauen Quadrat PHFC, die die Ecke F gemeinsam haben. Vorausgesetzt ist noch: P ist ein beliebiger Punkt auf der Strecke [OE].

O.b.d.A. nehmen wir die Seitenlänge des großen Quadrats als 1 an, sowie ein Koordinatensystem mit Ursprung O und den Einheitspunkten E bzw. G auf der x- bzw. y-Achse

Projiziert man die Diagonale [PF] senkrecht auf die y-Achse, so erhält man die Strecke [OG] mit der Länge 1.
Die andere Diagonale [HC] erhält man durch Rotation von [PF] um +90° (Zentrum M).
Daher muss die senkrechte Projektion von [HC] auf die x-Achse ebenfalls die Länge 1 haben:
LK = 1.

Da auch [OE] = 1 ist, folgt: [OL] = [EK].

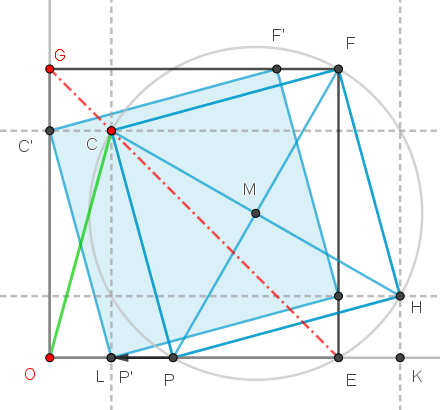
Verschiebt man nun das blaue Quadrat PHFC um OL nach links, so kommen C und H auf die Seiten des großen Quadrats zu liegen. (Das verschobene Quadrat P'H'F'C' ist von vier kongruenten rechtwinkligen Dreiecken umgeben, die in den Katheten übereinstimmen.)

Insbesondere folgt: P' = L, d.h. das Dreieck OPC ist gleichschenklig, somit ist OC = PC.

[OC] ist nun aber die Diagonale des grünen Dreiecks, also um den Faktor $$\sqrt{2}$$ länger als dessen Seite. Die Seitenlänge der beiden Quadrate verhalten sich also wie $$1:\sqrt{2}$$, ihre Flächeninhalte daher wie 1 : 2 oder 16 : 32.

🖖 Stay hard! Stay hungry! Stay alive! Stay home!