Mathematik zum Schokoladenstreit – Lösung

[Gunnar Bittersmann]

@@Gunnar Bittersmann

(Für dies „key insight“ muss man aber nicht die Vektorrechnung bemühen; das lässt sich auch geometrisch zeigen. @Tabellenkalk⁠s Herleitung begann mit „Wie man leicht sieht“ – da schrillten bei mir erstmal die Alarmglocken. 🤯 Man kann’s aber wirklich sehen.)

@Matthias Apsel hat auch nicht die Vektorrechnung bemüht, sondern Winkelfunktionen:

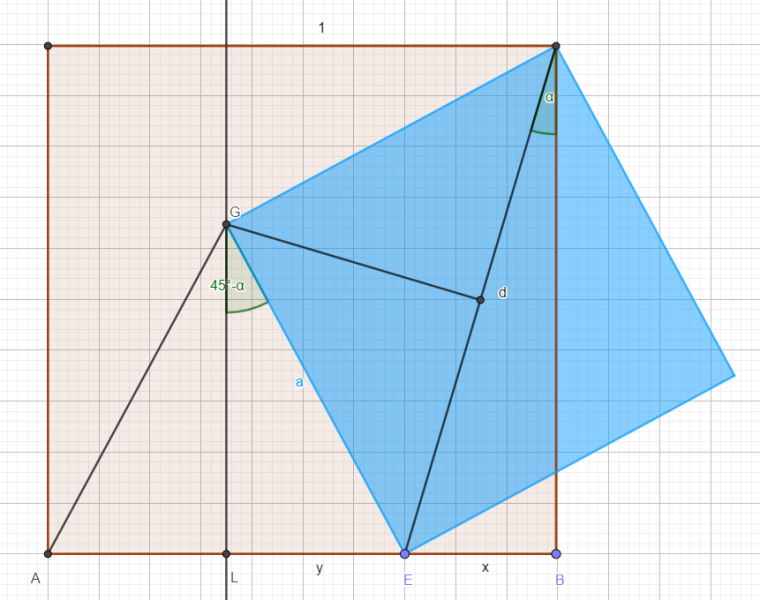
Das umgebende Quadrat habe die Seitenlänge 1, d ist die Diagonale des blauen Quadrats, a seine Seitenlänge. Die Strecke AG ist die Diagonale des grünen Quadrats.

Es gilt: d = 1/cos(α) und x = tan(α).

$$a = \frac{1}{2}\sqrt{2}d$$

$$\sin(45°-α) = \frac{y}{a}$$

$$y=\frac{1}{2}\sqrt{2}\cdot d \cdot \sin(45°-α)$$

$$y=\frac{1}{2}\sqrt{2}\cdot \frac{1}{\cos(α)} \cdot \frac{1}{2}\sqrt{2} (\cos(α)-\sin(α))$$

$$y=\frac{1}{2}\cdot \frac{1}{\cos(α)} \cdot (\cos(α)-\sin(α))$$

$$y=\frac{1}{2}\cdot (1-\tan(α))$$

Wie man leicht prüft, ist 2y + x = 1. Damit ist das Dreieck AEG gleichschenklig und somit die Diagonalenlänge des grünen gleich der Seitenlänge des blauen und das blaue mithin doppelt so groß wie das grüne.

Anmerkung von mir: Funktionsbezeichner sollten nicht kursiv gesetzt werden. In LaTeX \sin, \cos, \tan etc. verwenden.

🖖 Stay hard! Stay hungry! Stay alive! Stay home!