Hallo Matthias,
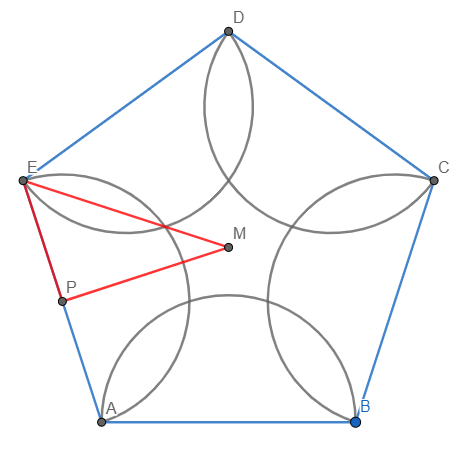
mein Ansatz war etwas anders, läuft aber auf's gleiche hinaus. Ich habe das rote Teildreieck im Fünfeck betrachtet.
Hier nochmal (das Bild ist zu einem anderen Zeitpunkt entstanden darum heißen die Punkte anders):
Die blauen Flächen bestehen aus dem Teil des Viertelkreises, der über das Dreieck hinausragt. Die orangen Flächen bestehen aus dem Teil des Dreiecks, das über den Viertelkreis hinausragt. Die Figur von Matthias enthält diese Flächen jeweils zehnmal, das kürzt sich bei der Verhältnisbildung heraus. Ich muss also nur mein Detailbild betrachten. Allerdings ist die Welt dann etwas komplizierter...
Ich schreibe jetzt nicht alle Formeln ab, letztlich berechne ich
- $$r_i$$ - den Inkreisradius des Fünfecks (gemäß Formel bei Wikipedia)
- A - die Fläche des roten Dreiecks als $$\frac{1}{2}a r_i$$
- K - den 72° Kreissektor um M von C nach Q als $$\pi a^2 \frac{72}{360}=\frac{\pi}{5}a^2$$
- S - das gleichschenkliche Dreieck MCQ als $$\frac{1}{2}a^2 \sin 72°$$
- Die Differenz K-S als Fläche des Kreissegments
- B - den 18° Kreissektor um M von Q nach P, das ist ein Viertel von K
- X - die Fläche des Dreiecks-Überstandes, als A - S - B.
Bei der Verhältnisbildung kürzt sich a heraus, das Verhältnis ist damit definitiv unabhängig von der Größe des Fünfecks.
Für das Verhältnis komme ich ebenfalls auf Matthias Wert.
Ich würde ja gern an $$\frac{8}{7 \pi}$$ als exakten Wert glauben, aber die Abweichung ist zu groß für einen IEEE-Rundungsfehler.
Rolf
sumpsi - posui - obstruxi