@@Gunnar Bittersmann
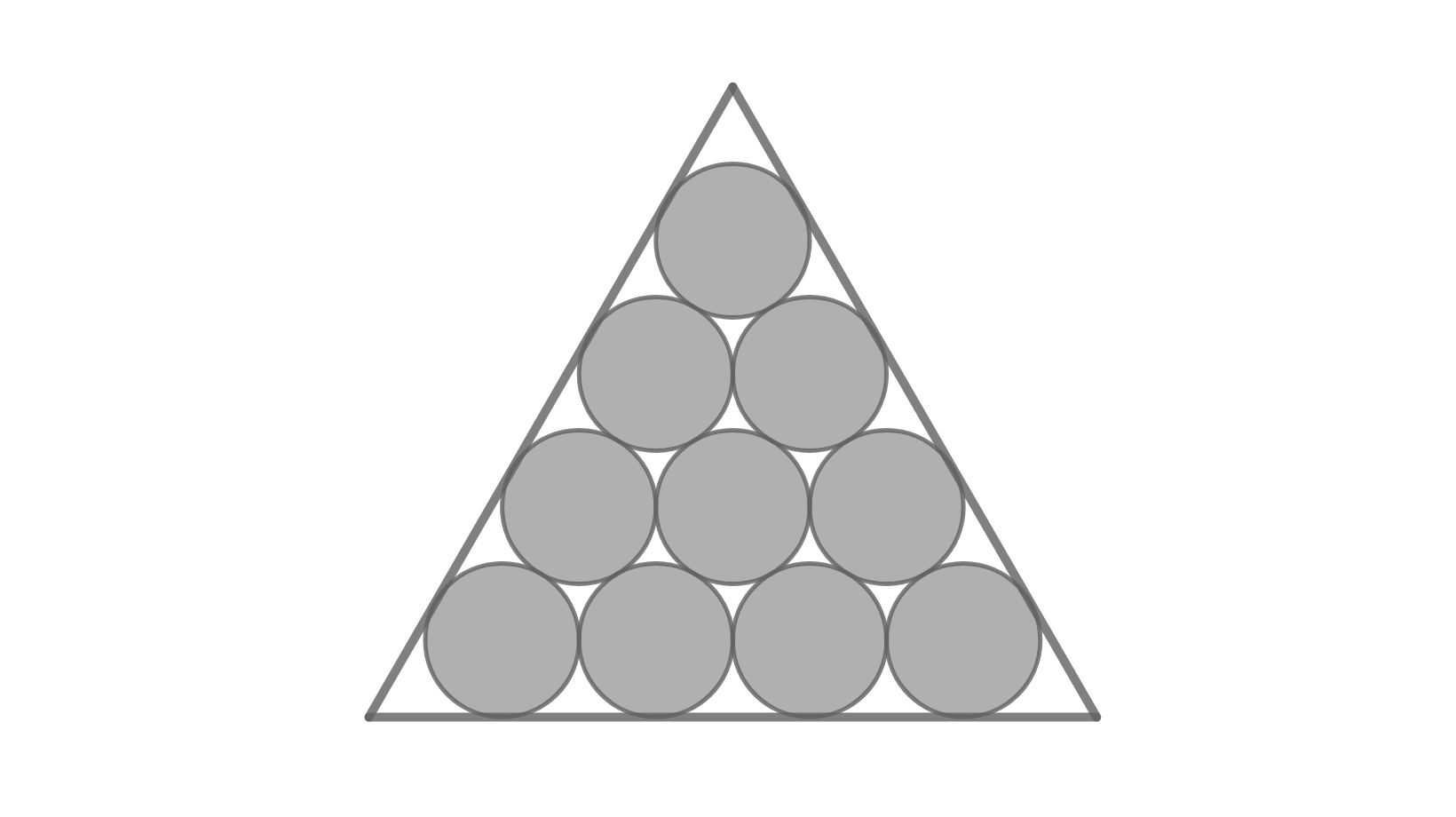
Wie ist das Verhältnis der schraffierten Fläche der Kreise zur Fläche des Dreiecks für n → ∞?
Man sieht, dass am Rand mehr von Kreisen unbedeckte Fläche bleibt als in der Mitte. Mit wachsendem n schwindet der Einfluss des Randes; für unendlich viele n gibt es keinen Rand mehr. Wir müssen uns also nur die Mitte ansehen; die Ebene wird mit dieser Figur parkettiert:
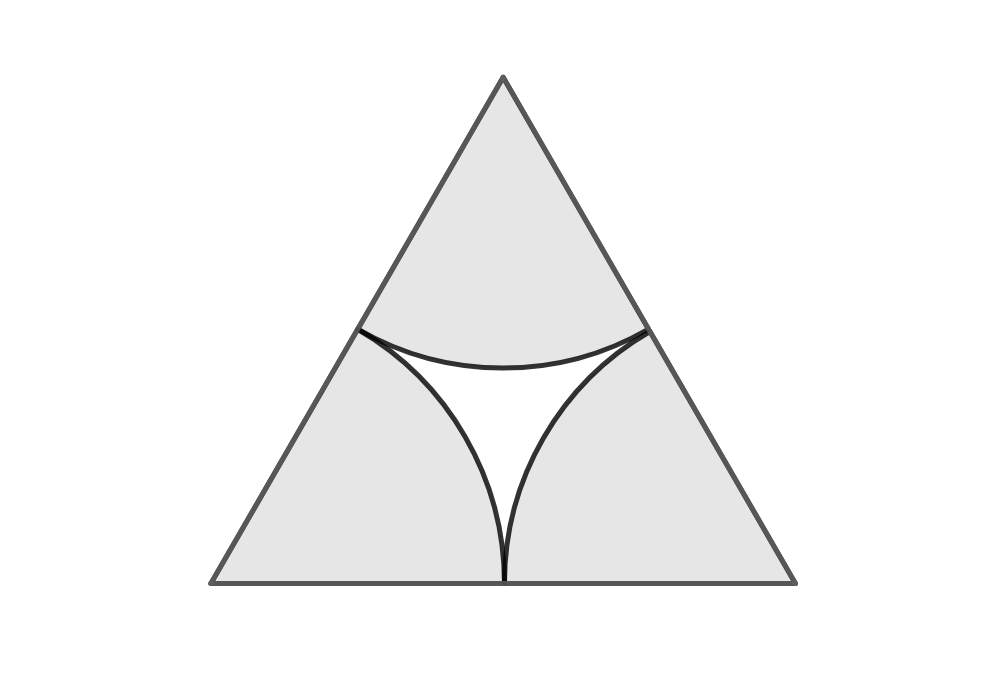
Drei Sechtelkreise machen einen Halbkreis; Fläche ½πr². Die Fläche des gleichseitigen Dreiecks mit Kantenlänge 2r ist r²√3. Das Verhältnis ist also ½π/√3 = ⅙π √3 ≈ 90.69%.
😷 LLAP
PS: Die (allgemeine) Lösung für Aufgabe 2 hab ich auch noch nicht.
--
„Sag mir, wie Du Deine Maske trägst, und ich sage Dir, ob Du ein Idiot bist.“ —@Ann_Waeltin
„Sag mir, wie Du Deine Maske trägst, und ich sage Dir, ob Du ein Idiot bist.“ —@Ann_Waeltin