outing – Lösung

[Gunnar Bittersmann]

@@Matthias Apsel

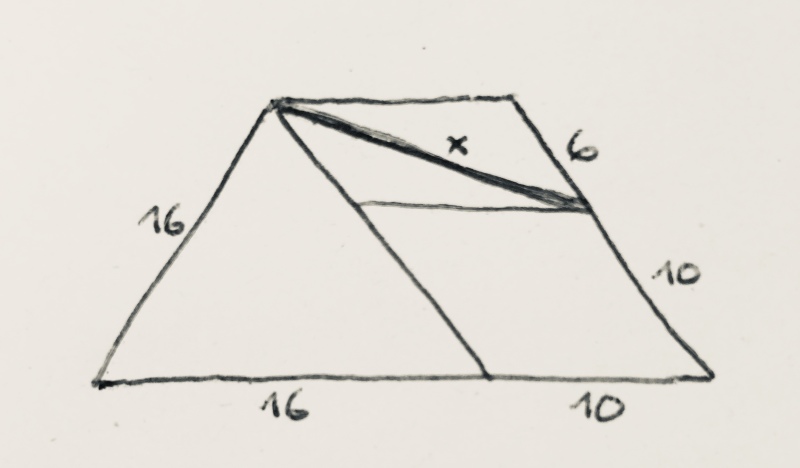
Die Parallele zum Schenkel teilt das Trapez in ein gleichschenkliges Dreieck und ein Parallelogramm. Da die Basis des Dreiecks ebenfalls 16 lang ist, ist es gleichseitig. Die gesuchte Länge ist also die längere Diagonale in einem Parallelogramm mit den Seitenlängen 6 und 10 und den Innenwinkeln 60° und 120°. (Mit Cosinussatz wäre es nun ein Leichtes, aber das wollen wir ja nicht.)

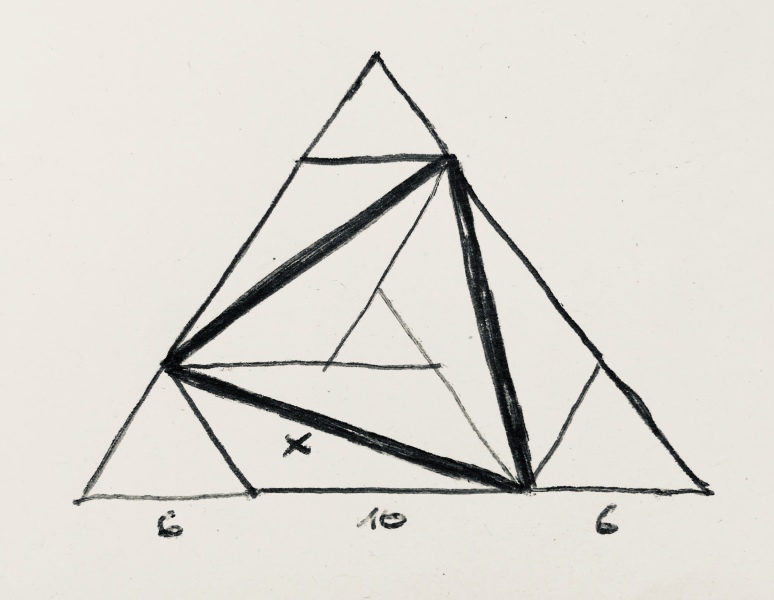
Von diesen Parallelogrammen nehmen wir drei und setzen sie wie gespoilert zusammen. Die Spitzen füllen wir mit gleichseitigen Dreiecken der Seitenlänge 6 auf und erhalten ein gleichseitiges Dreieck der Seitenlänge 22.

Der Flächeninhalt von ähnlichen Figuren hängt quadratisch von deren Längen ab: A = p · a² – p ist dabei sowas wie ein Formfaktor: für Quadrate der Seitenlänge a ist p = 1; für Kreise mit Radius a ist p = π; für gleichseitige Dreiecke der Seitenlänge a ist p irgendwas mit ’ner Wurzel (was Grundschüler nicht kennen). Wie schon genug gespoilert muss man aber den Wert von p überhaupt nicht kennen. Wie wir gleich sehen werden, kürzt der sich weg.

Der Flächeninhalt des großen Dreiecks beträgt p · 22²; der der Spitzen p · 6². Die anderen Randdreiecke haben dieselbe Höhe, aber eine um ¹⁰⁄₆ größere Grundseite, also den Flächeninhalt p · ¹⁰⁄₆ · 6². (¹⁰⁄₆ nicht zu ⁵⁄₃ kürzen!) Das innere Dreieck hat den Flächeninhalt p · x².

p · 22² = 3 · p · 6² + 3 · p · ¹⁰⁄₆ · 6² + p · x². Durch p geteilt(!) und Zahlen addiert ergibt x² = 196; x = 14.

😷 LLAP