Dreikönigsmathematik

[ottogal]

Ja, ich mag es gern kurz und knackig - und das heißt halt, dass man manchmal einen nicht ganz so elementaren Satz heranzieht...

Aber so mag es ja Catriona Agg auch in ihren Fragestellungen - die Voraussetzungen spricht sie nicht alle aus (man "sieht" sie schon...).

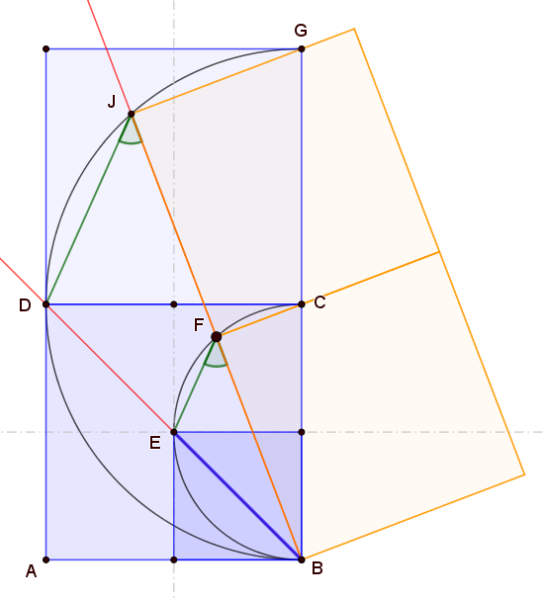
Hier sind es ja nicht einfach 3 Quadrate. Sie liegen in ganz bestimmter Weise zueinander, aber nicht eindeutig: Die gemeinsame Seite der beiden kleineren Quadrate muss durch die Ecke C des größeren Quadrats gehen.

Worauf kommt es also an? Dass das Dreieck BCF bei F einen rechten Winkel hat.

Bei dem Stichwort sollte einem immer der Satz von Thales einfallen (der ihm natürlich nicht als Spezialfall des Peripheriewinkelsatzes untergekommen ist, sondern wohl schlicht anhand der Symmetrien eines Rechtecks mit Umkreis).

Somit liegt F auf dem Thales(halb)kreis über BC.

Nun verwenden wir wieder das gehabte Argument: Der Winkel EFB ist Peripheriewinkel zur Sehne EB des Thaleskreises. Deren Mittelpunktswinkel ist ein rechter, folglich hat EFB 45°.

Und dann braucht man nur zu "sehen", dass das Dreieck DJB das Bild des Dreiecks EFB bei der Zentrischen Streckung mit Zentrum B und Streckfaktor 2 ist, und zu wissen, dass dies eine winkeltreue Abbildung ist... (Oder man macht zuerst die Streckung und argumentiert im Kreis um C wie gehabt.)