Mathematik zum Wochenanfang - Lösung

[ottogal]

Dank an alle, die mitgedacht haben...

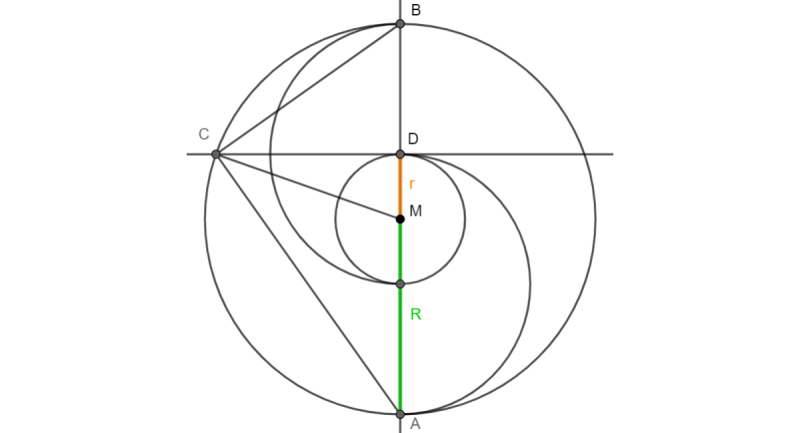
Sei $$r$$ der kleinste der Halbkreisradien, $$R$$ der größte.

Natürlich hängt $$R$$ von $$r$$ ab: Wegen der Voraussetzung $$CD = 2$$ gilt

$$R² - r² = 4$$.

Dies ergibt sich etwa im $$\triangle{CMD}$$ nach Pythagoras.

Oder man betrachtet $$\triangle{ABC}$$:
Da $$AB$$ Kreisdurchmesser ist, ist $$\angle{ACB}$$ ein rechter Winkel; der Höhensatz liefert $$CD² = AD \cdot DB$$, also $$4 = (R + r)(R - r) = R² - r²$$.

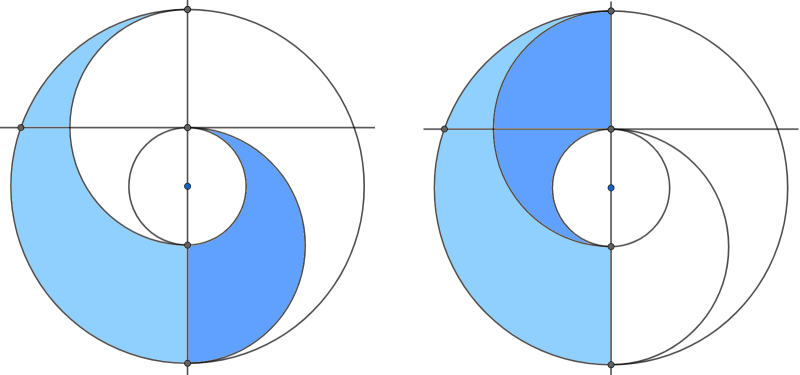
Für die gesuchte Fläche kann man die beteiligten Halbkreisflächen berechnen, Differenzen davon bilden und addieren. Man erhält so

$$\frac{\pi}{2} (R² - r²)$$, also $$\frac{\pi}{2} \cdot 4 = 2 \pi$$.

Es geht auch etwas eleganter:

Man dreht den dunkler gefärbten Teil der Figur um 180° um den Mittelpunkt M und erhält zusammen mit dem helleren Teil einen halbierten Kreisring, dessen Fläche gleich der der ursprünglichen Figur ist.
Also beträgt sie

$$\frac{1}{2} (\pi R² - \pi r²) = \frac{\pi}{2} (R² - r²) = 2 \pi$$.

Interessant an dem Ergebnis ist, dass es nicht vom Wert von $$r$$ (bzw $$R$$) abhängt:

https://www.geogebra.org/m/ek97rmtc

In diesem Geogebra-Blatt kann man den gemeinsamen Mittelpunkt (grün) auf der Vertikalgeraden verschieben (sogar über die rote Strecke hinaus) - der Flächeninhalt der blau umrandeten Figur bleibt stets gleich...

Richtige Lösungen haben (bisher) @Rolf B , @Gunnar Bittersmann , @Tabellenkalk und @encoder mitgeteilt.