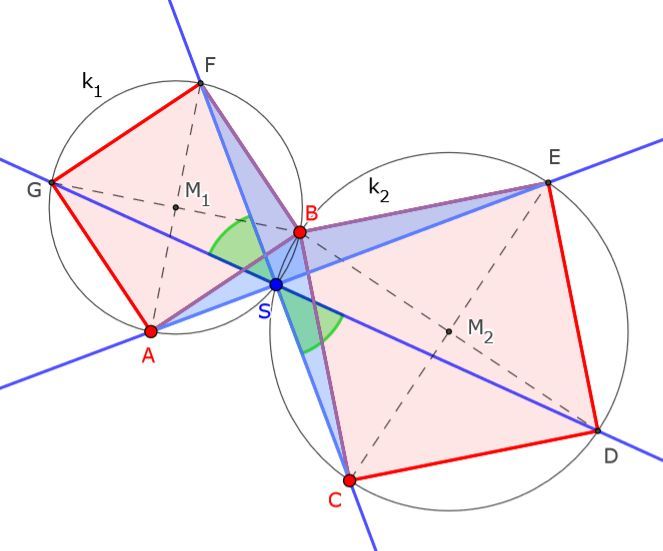
Teil-Lösung:
In der hier verlinkten Geogebra-Zeichnung
https://www.geogebra.org/m/ytuepgp6
lassen sich die roten Punkte A, B und C verschieben.
Dreht man das $$\triangle{AEB}$$ mit Drehpunkt $$B$$ um 90° im Uhrzeigersinn, so erhält man das $$\triangle{FCB}$$.
Dabei ist auch die Gerade $$AE$$ um 90° gedreht worden auf die Gerade $$FC$$; die beiden Geraden stehen also aufeinander senkrecht. Ihren Schnittpunkt nennen wir $$S$$. Es gilt also insbesondere $$\angle{FSA} = \angle{CSE} = 90°$$.
Zu zeigen bleibt: Die Punkte $$D$$, $$S$$ und $$G$$ liegen auf einer Geraden.
Man betrachte die Umkreise $$k_1$$ bzw. $$k_2$$ der Quadrate $$ABFG$$ und $$BCDE$$ mit ihren Mittelpunkten $$M_1$$ bzw. $$M_2$$.
Wir verwenden den Zusammenhang zwischen Umfangswinkel $$\phi = \angle{APB}$$ und Mittelpunktswinkel $$\mu = \angle{AMB}$$ einer Kreis-Sehne $$[AB]$$
(so genannter Kreiswinkelsatz):
Genau dann liegt $$P$$ auf der Kreislinie, wenn $$\mu = 2 \cdot \phi$$ ist:
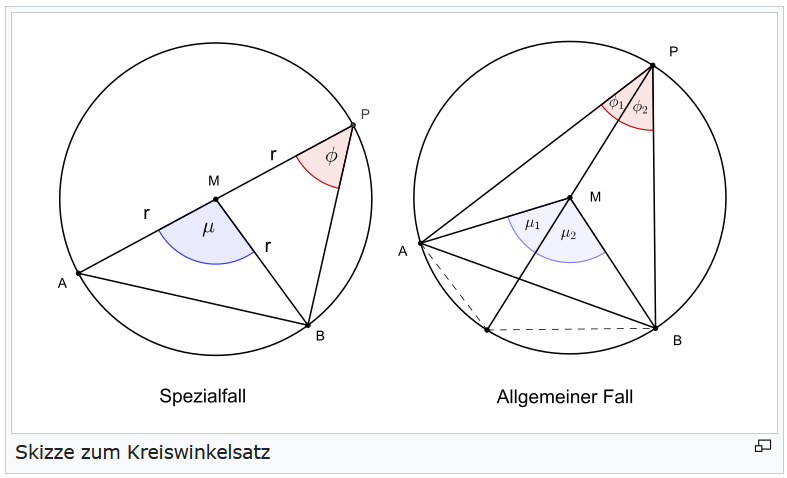
(Siehe Kreiswinkelsatz_(Zentriwinkelsatz) ).
Der Thales-Satz und seine Umkehrung sind ein Spezialfall hiervon: Falls $$[AB]$$ Durchmesser ist, wird $$\mu = 180°$$, und $$C$$ liegt genau dann auf der Kreislinie, wenn $$\phi = 90°$$ ist.
Damit ziehen wir folgende Schlüsse:
Weil $$[FA]$$ Durchmesser von $$k_1$$ und $$\angle{FSA} = 90°$$ ist, muss $$S$$ auf $$k_1$$ liegen.
Im Kreis $$k_1$$ gehört zur Sehne $$[FG]$$ der Mittelpunktswinkel $$\angle{FM_1G} = 90°$$,
also der Umfangswinkel $$\angle{FSG} = 45°$$.
Weil $$[CE]$$ Durchmesser von $$k_2$$ und $$\angle{CSE} = 90°$$ ist, muss $$S$$ auf $$k_2$$ liegen.
Im Kreis $$k_2$$ gehört zur Sehne $$[CD]$$ der Mittelpunktswinkel $$\angle{CM_2D} = 90°$$,
also der Umfangswinkel $$\angle{CSD} = 45°$$.
Es ist also $$\angle{FSG} = \angle{CSD}$$, und weil $$C$$, $$S$$ und $$F$$ auf einer Geraden liegen, muss das auch für $$D$$, $$S$$ und $$G$$ gelten.
Anmerkung:
Die Argumentation bleibt gültig, solange man in der abgebildeten Ausgangslage z.B. den Punkt $$C$$ nur so weit bewegt, dass $$S$$ auf dem Bogen $$AB$$ (ohne Endpunkte) bleibt.
Für andere Fälle muss man die Beweisführung modifizieren.
Dies sei dem interessierten Leser als (mühselige) Übung überlassen...