Mathematik zum Jahresanfang – Lösung

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Ja, bei dieser Aufgabe kommt man mit Plus und Minus natürlicher Zahlen bis 5 aus.

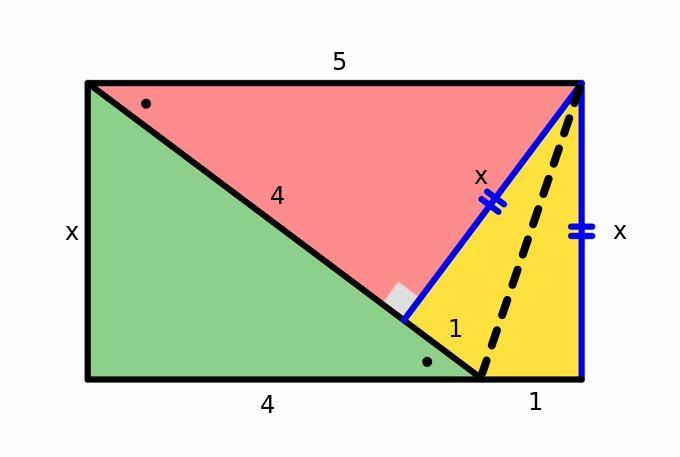
Wenn man die Symmetrieachse des gelben Drachenvierecks einzeichnet, sieht man, dass die beiden Dreiecke nach SSW kongruent sind.

Damit es möglichst einfach wird, setzen wir die nicht markierte (die kurze) Seitenlänge des Drachenvierecks o.B.d.A. gleich 1. Die markierte lange Seite hat die Länge x.

Das Drachenviereck hat die Fläche eines Rechtecks mit Grundseite 1 und Höhe x. Das 5 Mal so große Rechteck derselben Höhe hat also die Grundseite 5.

Weiterhin sieht man, dass das rote und das grüne Dreieck nach WSW kongruent sind. Es sind rechwinklige Dreiecke mit Hypothenuse 5 und Katheten 5 − 1 = 4 und x. Da wir (3, 4, 5) als pythagoräisches Tripel kennen, müssen wir nicht quadrieren und Wurzel ziehen. x = 3.

Das Seitenverhältnis ist also 3 : 5 – als Verhältnis benachbarter Fibonacci-Zahlen nah am goldenen Schnitt.

Und es ist dasselbe Verhältnis wie bei Schwarz-Rot-Gold 🇩🇪. Auch die DDR-Fahne^[1] hatte dieses Seitenverhältnis. Und auch vom Union Jack 🇬🇧 gibt es eine 3 : 5-Version; wie auch dessen Bestandteile englische und schottische Flagge dieses Verhältnis haben.

Aufgabe von @panlepan; Lösung von @MatthewArcus

🖖 Живіть довго і процвітайте

---

1. Ja, ich weiß, dass es eigentlich „Flagge“ heißt. Wir haben aber früher immer „Fahne“ gesagt. ↩︎