Mathematik zum Wochenanfang – Lösung

[ottogal]

Hallo in die Runde!

Man wendet im Prinzip dreimal einen Hilfssatz an, jeweils bezogen auf 2 der 3 fraglichen Kreise:

Hilfssatz:

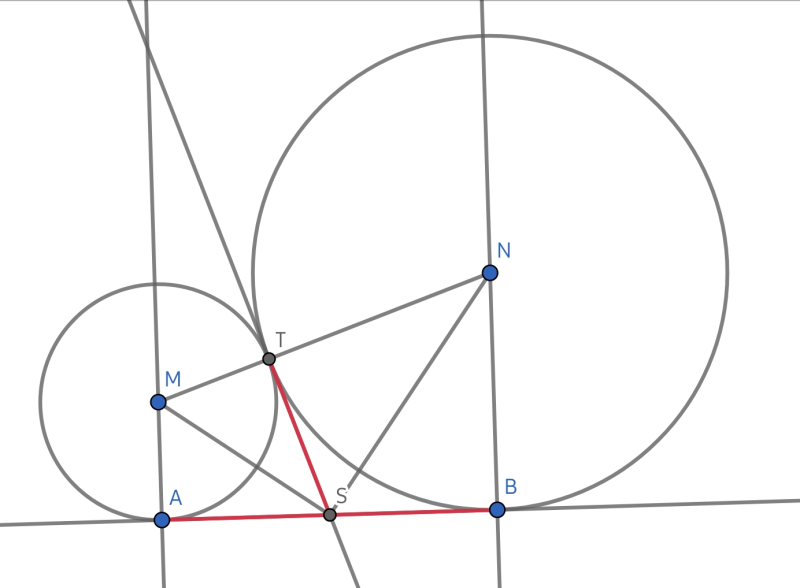
Gegeben sind zwei Kreise mit der gemeinsamen Tangente AB, die sich im Punkt T berühren und die Radien a = MA und b = NB haben.
Dann gilt: Die Strecke AB hat die Länge
2√(ab).

Das lässt sich (wie von Gunnar) mit Pythagoras beweisen:
AB² = (b + a)² −  (b − a)² = 4ab, also
AB = 2√(ab).

Pythagoras ist halt immer etwas langweilig - deshalb noch ein Beweis ohne ihn (dafür mit Höhensatz):

Die Tangente durch T an beide Kreise schneidet AB in S. Die (roten) Tangentenabschnitte SA, ST und SB haben alle die gleiche Länge t, und die Dreiecke SMA, SMT, SNT und SNB sind alle rechtwinklig und haben jeweils die gleichen spitzen Winkel $$\alpha$$ und $$\beta$$ (mit $$\alpha+\beta=90°$$).

Der Winkel $$\angle{NSM}$$ hat folglich ebenfalls 90°.
Der Höhensatz im Dreieck NMS liefert nun

t² = ab, also t = √(ab).

Somit ist AB = 2t = 2√(ab).

Zur eigentlichen Aufgabe:

Der gesuchte Kreis habe den Radius r und berühre AB im Punkt C.
Wir wenden den Hilfssatz dreimal an:
Mit a = 2 und b = r:
Es folgt AC = 2√(2r).
Mit a = r und b = 4:
Es folgt CB = 2√(4r) = 4√r
Mit a = 2 und b = 4:
Es folgt AB= 2√8 = 4√2
Wegen AC + CB = AB folgt (nach Division durch 2):
√(2r) + 2√r = 2√2.
Diese Gleichung lässt sich nach r auflösen:
√r (√2 + 2) = 2√2
√r (2 + √2) (2 − √2) = 2√2 (2 − √2)
√r (4 − 2) = 4√2 − 4
√r = 2√2 − 2
r = 8 − 8√2 +4
r = 12 − 8√2.

Viele Grüße aus dem Urlaub
ottogal